복습 정리 노트

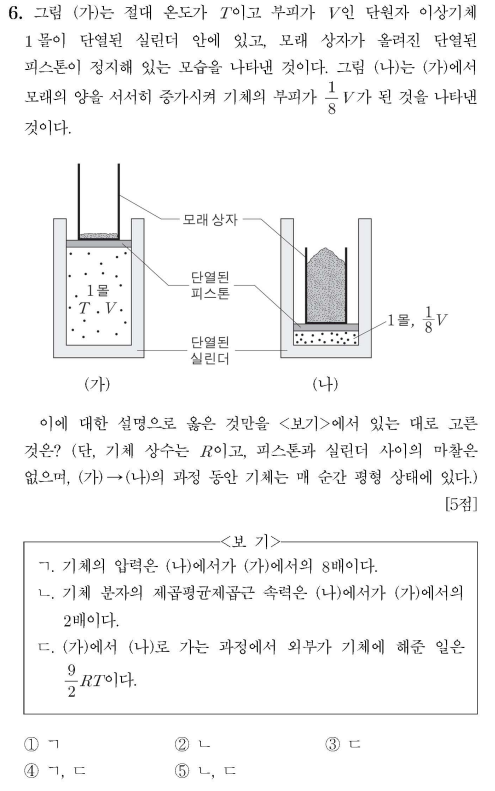
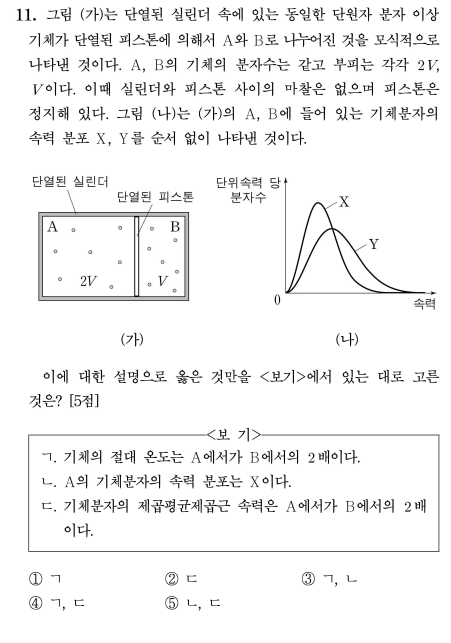
오늘부터는 일반화학 핵심개념과 관련된 어려운 문제들도 좀 풀어보면서 실전 문제풀이 능력을 기르고 약점을 보완해보도록 하겠습니다. 먼저 화학반응식 관련 문제부터 보고 갑시다. 문제 계수비가 알려지지 않은 반응식을 주고 보기의 사실관계를 파악하는 문제입니다. 계수비를 먼저 찾아준 뒤, 각각의 비율을 이용하여 생성물의 질량이나 압력 등을 확인해볼 수 있는 문제입니다. 풀이 먼저 반응식의 계수부터 맞춰줍니다. 수소의 경우 반응물과 생성물 모두에서 하나의 화합물만 가지고 있으므로 수소 먼저 맞춰줍시다. 그 다음 F의 비율을 맞춰주고, 마지막으로 Eu의 비율을 맞춰주면 순서대로 2Eu + 6HF -> 2EuF3 + 3H2의 계수비가 만들어짐을 알 수 있습니다. 보기 ㄱ에서는 계수비 b/a의 값을 묻고 있으므로 확인..

문제 단열 피스톤에 의해 분리된 실린더의 한 쪽만을 가열했을 때 변하는 부피를 알려주고 양쪽의 온도 변화나 압력 변화 등을 구해보는 문제입니다. 풀이 가운데의 피스톤이 단열이라고 하였으므로 왼쪽을 가열해도 오른쪽 B는 여전히 단열상태입니다. 따라서 B는 단열압축된다는 사실을 알 수 있고 따라서 PV^gamma는 일정이라는 공식을 사용할 수 있습니다. 보기 ㄱ에서 압력 변화에 대하여 물어봤으므로 같은 공식을 대입하여 계산해주면 보기 ㄱ이 맞다는 사실을 알 수 있습니다. 보기 ㄴ을 보면 A와 B의 절대온도에 대하여 묻고 있습니다. 우선 B는 단열압축과정을 거쳤기 때문에 단열 조건을 사용하여 T_B는 공식을 그대로 이용하여 계산해줄 수 있습니다. 그러나 A는 열이 분명 가해졌기 때문에 단열이라든지 어떤 조건을..

문제 단열 피스톤으로 분리된 공간을 외부에서 모래의 양을 증가시키면서 압축을 가하는 단열 압축 문제를 해결해봅시다. 풀이 가장 먼저 단열이라는 키워드가 눈에 띄어야합니다. 단열 압축 과정이고 보기 ㄱ에서는 압력비에 대한 질문을 하였으므로 PV^gamma가 일정하다는 공식을 이용하여 문제를 풀어주면 됩니다. 따라서 위와 같은 식을 세워주면 나중 압력이 처음 압력의 32배임을 알 수 있습니다. 보기 ㄴ에서는 근평균제곱속력에 대해서 묻고 있습니다. 그런데 v_rms는 절대온도의 제곱근에 비례하기 때문에 절대온도의 비를 구해주는 것이 우선입니다. 단열과정의 경우 TV^(gamma-1) = 일정이라는 공식 또한 존재하기 때문에 이를 역시 적용해주면 온도는 4배가 됨을 알 수 있고, 따라서 이것에 제곱근을 씌워준 ..

문제 오른쪽 공간이 진공 상태일 때 판을 갑자기 제거하여 기체를 자유 팽창시키는 조건의 문제입니다. 보기들이 맞는지 확인해봅시다. 풀이 "자유" 팽창 문제의 핵심은 위와 같습니다. 기체가 판을 밀어서 사라진 것이 아니라, 판이 한순간에 사라졌다고 생각해보면 기체는 일을 해서 부피가 늘어난 것이 아니므로 W=0이며, 비가역과정에 해당합니다. 단열 팽창이므로 Q=0으로 두고 열역학 제1법칙을 사용해보면 에너지 변화량이 0이므로 온도 변화량도 0이 되어야합니다. 따라서 보기 ㄱ은 맞습니다. 보기 ㄴ의 경우 압력이 변화 전과 후가 같다고 하였는데 부피가 증가하였는데 W=0이 되려면 압력은 감소해야합니다. 따라서 보기 ㄴ은 틀렸다고 할 수 있습니다. 보기 ㄷ의 경우 엔트로피를 그냥 구할 수는 없는데요, 왜냐하면 ..

문제 피스톤으로 두 공간으로 나누어진 용기 내에서 한쪽만을 가열했을 때 두 공간에 있는 분자들의 이동속도 비를 구하는 문제를 풀이해봅시다. 풀이 우선 이동속도비를 구하라고 하였으므로 v_rms가 (T/M)^(1/2)에 비례한다는 사실을 리마인드하여 두 상황에서의 절대온도의 비를 구해야겠다는 사실을 인지하여야 합니다. (분자량의 경우 1:2라고 문제에서 제시해주었음) 먼저 (가)의 상황을 확인해보면, 피스톤 자체가 평형을 이루었다고 하였으므로 양쪽의 압력이 같음을 알 수 있습니다. 따라서 양쪽의 압력을 이상기체 상태방정식으로 나타내어보면 n_A:n_B가 1:2임을 알 수 있습니다. 여기서 문제를 조금이라도 빨리 푸는 팁은 몰수비만 알고 실제 몰수를 모른다고 하더라도 그냥 1mol, 2mol이라고 가정하고 ..

문제 단열된 실린더 내의 단원자 분자 이상기체가 왼쪽은 2V, 오른쪽은 V의 부피를 가지도록 피스톤에 의해 나뉘어져 있을 때 분자들의 속력에 대한 분포 그래프를 참고하며 푸는 문제입니다. 풀이 위에서 가장 중요한 조건은 "실린더와 피스톤 사이의 마찰이 없다"는 것입니다. 따라서 피스톤은 압력이 높은 쪽에서 낮은 쪽으로 밀려나므로 결국 양쪽의 P가 같다는 조건이 발생합니다. 이 때 피스톤을 제거하더라도 용기 전체의 부피와 분자의 수는 일정하므로 압력은 역시 그대로입니다. 따라서 압력을 다른 식으로 나타낸 뒤 그 압력들이 모두 같다고 식을 세우면, T_A는 T_B보다 2배 큰 온도를 가지고 있음을 알 수 있고 따라서 보기 ㄱ은 맞음을 알 수 있습니다. 그 다음에는 분자들의 속력 분포에 대한 그래프를 이용해 ..

문제 단열 용기속 단원자 이상기체를 단열판으로 나누어 둔 초기상태에서 단열판을 제거했을 때의 상태 변화에 대해서 묻는 문제입니다. 풀이 우선 문제에서 조건을 기체의 몰수가 아닌 분자수로 주었으므로 분자수 N에 대한 기호로 바꾸어 생각해야 합니다. 그러면 P=NkT/V라는 관계식을 얻을 수 있고, 기체 에너지 U = 3/2 NkT = 3/2 PV로 나타낼 수 있는 사실도 알 수 있습니다. 문제 조건에서 판을 제거하기 전과 제거한 후의 전체 부피가 같다는 조건을 우선 참고해두고, 단열판 제거 전과 후의 기체 에너지가 같다는 등식을 세워 문제를 풀어봅시다. 먼저 U = 3/2 PV임을 이용하여 P=NkT/V를 대입해줍시다. 그러면 판이 제거되기 전 양쪽 기체 에너지의 합은 24NkT가 됩니다. 그리고 나중 에..

문제 문제를 읽어보면 피스톤을 고정시키지 않고 외부 압력을 일정하게 유지시킨채로 온도에 변화를 주었으므로 등압조건이라고 할 수 있습니다. 등압조건에서의 열역학 문제를 해결해봅시다. 풀이 우선 이상기체 상태방정식에서 응용된 식인 PV/T = 일정을 이용하여 나중 온도를 구해보면 나중 온도는 2T_0임을 알 수 있습니다. 그 다음 문제가 등압조건이므로 W = P delta V = nR delta T임을 이용해주면 기체가 외부에 한 일은 RT_0임을 알 수 있습니다. 보기 ㄴ에선느 기체의 평균 운동에너지에 대해서 묻고 있는데 기체의 평균운동에너지는 3/2 kT이므로 오직 절대온도에만 비례하는 수치입니다. 온도가 실제로 T_0에서 2T_0로 두 배 증가하였으므로 보기 ㄴ은 맞음을 알 수 있습니다. 보기 ㄷ에서는..

문제 두 종류 이상의 재질로 구성된 막대의 열 전도 문제입니다. 열은 온도가 높은 열원에서 온도가 낮은 열원으로 이동하며 이 때 열의 전도량은 열 전도 상수, 접촉면의 넓이, 온도 차이, 재질의 길이 등에 따라 달라집니다. 풀이 우선 보기 ㄱ은 아주 간단합니다. 열의 이동이 80W의 속도로 나타나므로 10초 지속될 경우 총 800J의 에너지가 전달되게 됩니다. 그 다음부터는 열의 이동량은 어느 지점에서든 같다(유체역학에서 사용되는 성질과 비슷하네요)를 이용하여 A의 단위 시간당 열의 전달량 = B의 단위시간당 열의 전달량 = 총 막대의 단위시간당 열의 전달량이라는 식을 세워 연립방정식을 풀어주면 됩니다. 그런데 중요한 점은 열의 전달량에 대한 식을 알아야한다는 것입니다. 또는 센스가 있다면 대략적으로 단..

문제 위처럼 관의 두께와 높이가 변화할 때 각각의 지점에서 압력과 유체의 속력 등을 구해보는 문제를 해결해봅시다. 풀이 공식은 크게 두 가지를 알면 다 풀 수 있습니다. 먼저 관을 같은 시간동안 지나는 유체의 부피는 어느 지점이든 동일하다는 점(Av = 일정), 그리고 베르누이 방정식(P + rho g h + 1/2 rho v^2 = 일정)을 이용하면 됩니다. 먼저 보기 ㄱ은 A 지점과 C 지점의 유체의 속도를 비교하고 있습니다. 따라서 Av는 일정이라는 조건을 이용하여 계산해주면 v_C = 4/9 v_0이므로 v_0보다 작고 ㄱ은 맞는 보기임을 알 수 있습니다. 보기 ㄴ은 두 지점의 압력차에 대해 논하고 있기 때문에 단순히 같은 관을 지나는 유체의 부피가 일정하다는 성질만으로는 풀 수 없습니다. 따라서..