문제

피스톤으로 두 공간으로 나누어진 용기 내에서 한쪽만을 가열했을 때 두 공간에 있는 분자들의 이동속도 비를 구하는 문제를 풀이해봅시다.
풀이

우선 이동속도비를 구하라고 하였으므로 v_rms가 (T/M)^(1/2)에 비례한다는 사실을 리마인드하여 두 상황에서의 절대온도의 비를 구해야겠다는 사실을 인지하여야 합니다. (분자량의 경우 1:2라고 문제에서 제시해주었음)

먼저 (가)의 상황을 확인해보면, 피스톤 자체가 평형을 이루었다고 하였으므로 양쪽의 압력이 같음을 알 수 있습니다. 따라서 양쪽의 압력을 이상기체 상태방정식으로 나타내어보면 n_A:n_B가 1:2임을 알 수 있습니다.
여기서 문제를 조금이라도 빨리 푸는 팁은 몰수비만 알고 실제 몰수를 모른다고 하더라도 그냥 1mol, 2mol이라고 가정하고 푸는 것입니다.
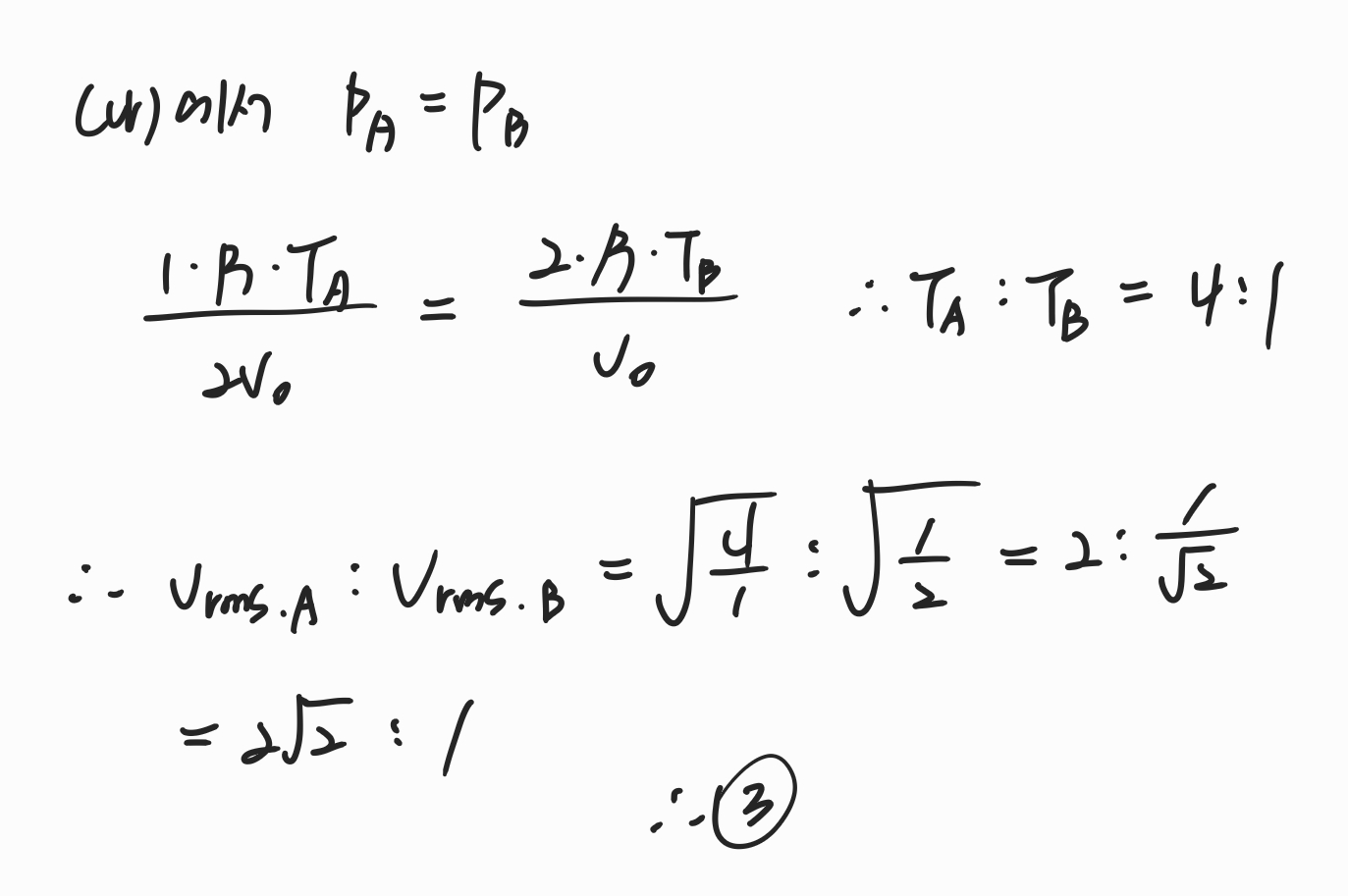
그 다음 (나)의 조건을 확인해보면 우리는 몰수비를 알기 때문에 온도비를 구할 수 있습니다. 따라서 구해보면 T_A:T_B=4:1임을 알 수 있고, 따라서 근평균제곱속력의 비가 2루트2:1임을 알 수 있습니다.
따라서 답은 3번입니다.

문제 상황에서 아주 유용한 정보를 또 얻을 수 있는데요, 바로 B의 내부에너지 증가량을 구해보는 것입니다.
내부에너지 증가량 delta U = 3/2 nR delta T이므로 변화 온도만 알고 있다면 구할 수 있습니다. (이 때 n은 그냥 위에서 풀다가 가정한대로 2mol이라고 가정합니다.)
그런데 가열 조건을 보면 단열 피스톤을 기준으로 왼쪽의 A만을 가열했으므로 B의 (가)->(나) 과정은 단열과정이 됩니다. 따라서 단열 조건 중 하나인 "TV^gamma = 일정"이라는 조건을 이용해주면, (나)의 B의 T가 2^(2/3) T_0임을 알 수 있습니다. 따라서 답은 B의 내부에너지 변화량은 위와 같습니다.
'자연과학(PEET) > 일반물리' 카테고리의 다른 글
| [열역학] 외부에서 일을 가하는 단열 압축문제 (2015학년도 6번 풀이) (0) | 2021.02.22 |
|---|---|
| [열역학] 판을 순간적으로 제거하는 단열 자유팽창 문제 (2012학년도 5번 풀이) (2) | 2021.02.22 |
| [열역학] 용기 내에서 고정 안된 판을 제거하는 문제 (2011학년도 5번 풀이) (0) | 2021.02.21 |
| [열역학] 용기 내에서 고정된 판을 제거하는 문제 (2011학년도 5번 풀이) (0) | 2021.02.21 |
| [열역학] 등압조건에서의 열역학 문제 (2013학년도 8번 풀이) (0) | 2021.02.21 |