반응형
문제

위처럼 관의 두께와 높이가 변화할 때 각각의 지점에서 압력과 유체의 속력 등을 구해보는 문제를 해결해봅시다.
풀이
공식은 크게 두 가지를 알면 다 풀 수 있습니다. 먼저 관을 같은 시간동안 지나는 유체의 부피는 어느 지점이든 동일하다는 점(Av = 일정), 그리고 베르누이 방정식(P + rho g h + 1/2 rho v^2 = 일정)을 이용하면 됩니다.

먼저 보기 ㄱ은 A 지점과 C 지점의 유체의 속도를 비교하고 있습니다. 따라서 Av는 일정이라는 조건을 이용하여 계산해주면 v_C = 4/9 v_0이므로 v_0보다 작고 ㄱ은 맞는 보기임을 알 수 있습니다.

보기 ㄴ은 두 지점의 압력차에 대해 논하고 있기 때문에 단순히 같은 관을 지나는 유체의 부피가 일정하다는 성질만으로는 풀 수 없습니다. 따라서 유체의 속도를 먼저 구해준 뒤 베르누이 방정식에 대입하여 두 지점의 압력차를 구해주어야 합니다.
위와 같은 식으로 계산하여 풀면 15/32 rho v_0^2이 나와 보기 ㄴ은 맞다는 것을 알 수 있습니다.
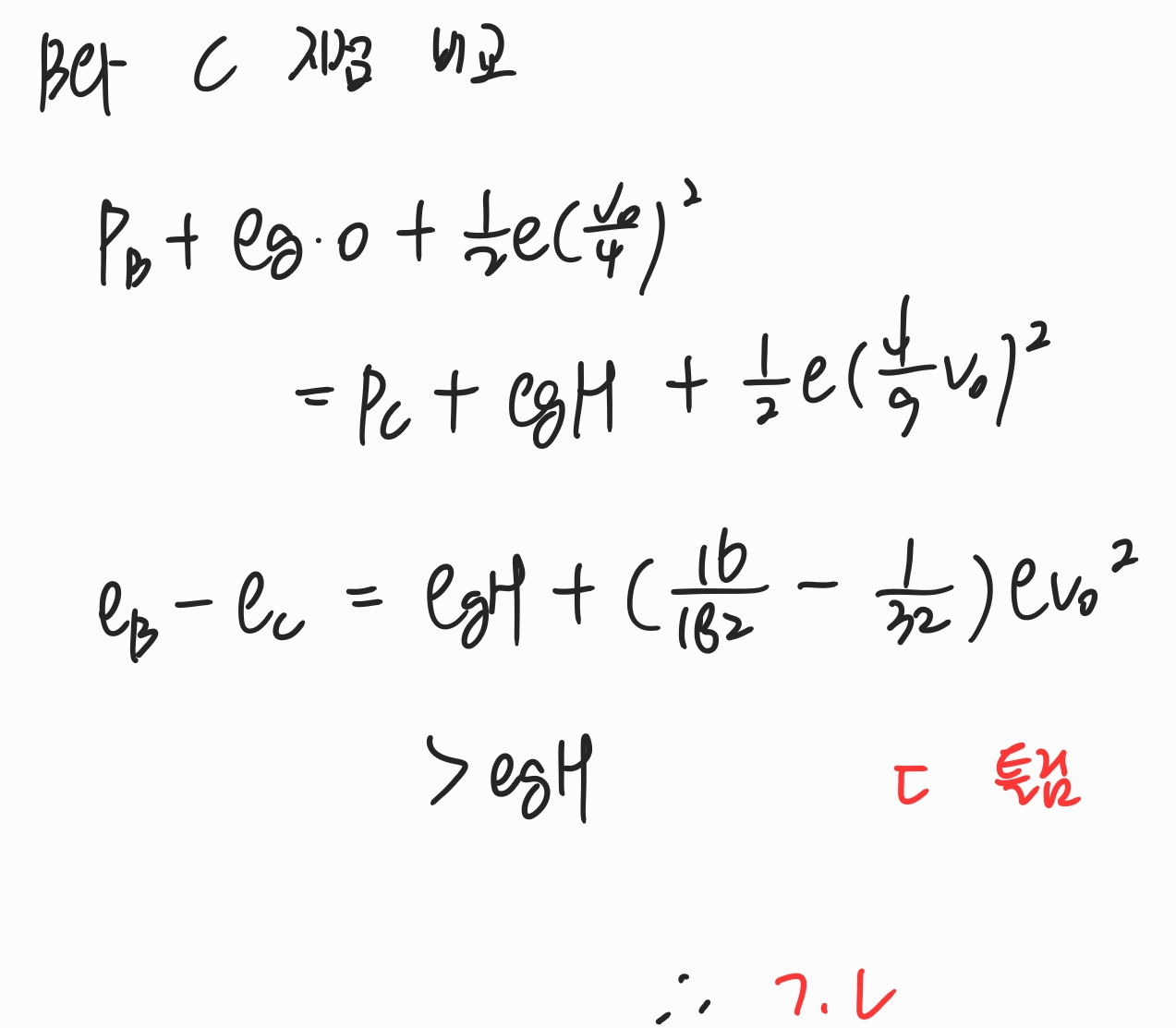
마지막으로 보기 ㄷ은 보기 ㄴ을 풀었다면 같은 원리로 풀어줄 수 있습니다. 똑같이 계산해보면 뒤의 분수식이 숫자가 조금 크게 나오는데, 이는 그냥 계산해줘도 되고 계산을 안하더라도 rho g H보다는 크다는 것을 알 수 있습니다. 따라서 정답은 ㄱ과 ㄴ에 해당합니다.
반응형
'자연과학(PEET) > 일반물리' 카테고리의 다른 글
| [열역학] 용기 내에서 고정된 판을 제거하는 문제 (2011학년도 5번 풀이) (0) | 2021.02.21 |
|---|---|
| [열역학] 등압조건에서의 열역학 문제 (2013학년도 8번 풀이) (0) | 2021.02.21 |
| [열역학] 두 개의 막대를 통한 열 전도 문제 (2016학년도 15번 풀이) (1) | 2021.02.21 |
| [역학] 용수철의 나무 도막이 분리되는 문제 (2018학년도 20번 풀이) (0) | 2021.02.21 |
| [역학] 포물선 운동이 포함된 일과 에너지 문제 (2014학년도 20번 풀이) (0) | 2021.02.21 |