문제

대전된 극이 서로 다른 선 전하 밀도가 주어진 두 개의 무한 선형 대전체가 있을 때, 특정한 좌표에서의 전기장의 합을 구하는 문제를 풀이해봅시다.
풀이
전기장을 구하는 문제는 점전하나 선전하가 주어졌을 때 보통 아무리 많이 주어져도 3개까지밖에 안 주어지기 때문에 문제 상황을 최대한 단순화시켜서 풀이해야합니다. 우선 다음과 같이 전기장의 합이 어떤 방향으로 나타날지 생각해봅시다.

+극으로 대전된 막대로부터는 멀어지는 방향으로 전기장이 작용하고, -극으로 대전된 막대로부터는 가까워지는 방향으로 전기장이 작용하며, (0, d, 0) 좌표는 두 대전체로부터 같은 거리에 위치한 점이기 때문에 전기장의 크기는 같습니다.
따라서 크기와 방향을 위처럼 y축에 대해서 대략적으로 나타내어보면 x축 양의 방향으로 루트 2배만큼의 전기장이 작용할 것임을 예상할 수 있습니다. 또는 문제의 보기를 보아도 대부분의 보기가 x축 양의 방향을 나타내고 있기 때문에 대략적으로 그렇게 전기장이 작용하겠구나 하고 예상이 쉽게 가능합니다.

그리고 이 식은 실전 풀이에서는 유도할 필요 없이 외우고 있으면 20~30초 정도 더 아낄 수 있겠지만, 만약 기억이 나지 않는다면 위와 같이 빨리 유도를 해서 풀이할 수 있어야합니다. 가우스 법칙에 의해서 선전하막대를 기준으로 원통형의 외부 표면을 잡으면 해당 표면에 수직 방향으로 나가는 전기장의 성분들을 모두 합치면 (이는 애초에 가우스 법칙에서 E와 dA 사이의 연산이 도트 곱이기 때문에 이렇게 연산이 되는 것입니다.) 위와 같이 되므로 원통의 길이는 서로 소거가 되고 전기장은 위와 같이 구해집니다.
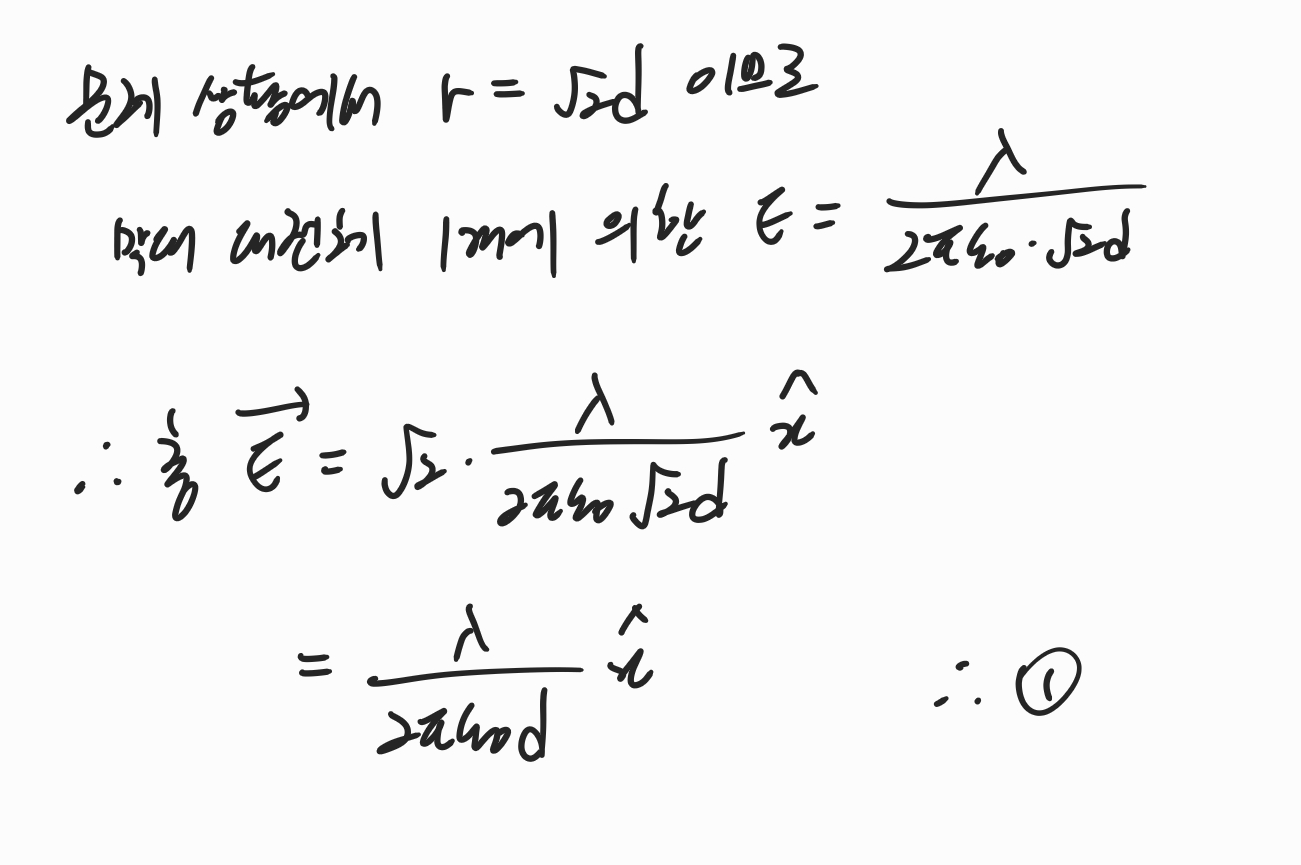
따라서 위에서 얻은 공식의 r 자리에 막대로부터의 거리인 루트2를 대입해주고, 전체 E는 그 크기의 다시 루트 2배이기 때문에 연산을 해주면 위와 같은 답이 나옴을 알 수 있습니다. 전기장은 벡터 성분이기 때문에 방향까지 나타내어주면 x축 양의 방향으로 작용하며 따라서 정답은 1번이 됩니다.
'자연과학(PEET) > 일반물리' 카테고리의 다른 글
| [축전기] 간단한 회로의 축전기에 충전되는 전기에너지 구하기 (2021학년도 7번 풀이) (0) | 2021.03.09 |
|---|---|
| [전기회로] 키르히호프의 법칙을 적용하여 각 점에서의 전류, 전위, 소모 전력 구하기 (2012학년도 11번 풀이) (0) | 2021.03.09 |
| [일과 에너지] 마찰이 있는 수평면에서의 용수철 운동에 관한 문제 (2015학년도 20번 풀이) (0) | 2021.03.09 |
| [전자기학] 전하가 균일한 절연체 내부에서의 전기장 구하기 (2021학년도 18번 풀이) (0) | 2021.03.06 |
| [열역학] 카르노 기관에서의 부피비, 열효율, 엔트로피에 대해 묻는 문제 (2017학년도 20번 풀이) (0) | 2021.03.06 |