2013학년도 9번


아세틸렌의 연소 반응식을 계수 없이 알려주고, 생성물 H2O의 질량을 알려준 뒤 설명에 대해 옳은 것을 고르는 문제입니다.
ㄱ, ㄴ. 쉽게 해결할 수 있습니다.
ㄷ. 0℃, 22.4L, 1mol 기체의 압력은 1atm으로 정의됩니다. (표준 상태인 25℃와 헷갈리지 않도록 주의합니다.)
이상기체 상태방정식을 응용하여 CO2의 분압을 계산하면 4.48atm임을 알 수 있습니다.
따라서 정답은 5번입니다.
2013학년도 14번


착이온과 배위화합물의 특성에 대해 묻는 문제입니다.
ㄱ. 평면사각형도 정팔면체와 같은 오비탈을 사용한다는 점을 유념하여 똑같이 t_2g, e_g 오비탈로 나뉨을 알아야 합니다.
d 오비탈 전자수는 28 - 18 - 2 = 8이므로 t_2g 오비탈 전자 수는 6개, e_g 오비탈 전자 수는 2개입니다.
ㄴ. 엔트로피는 분자 수를 통해 파악이 가능합니다.
반응식에서 전체 분자는 반응물에서 4분자, 생성물에서 7분자이므로 엔트로피 변화량은 양의 값을 가집니다.
ㄷ. [Nien_3]2+이 더 강한 리간드이므로 파장이 짧은 쪽이 A임을 알 수 있ㅅ브니다.
B는 [Ni(H2O)6]2+이므로 광학이성질체를 가지지 않습니다.
따라서 정답은 1번입니다.
2013학년도 19번
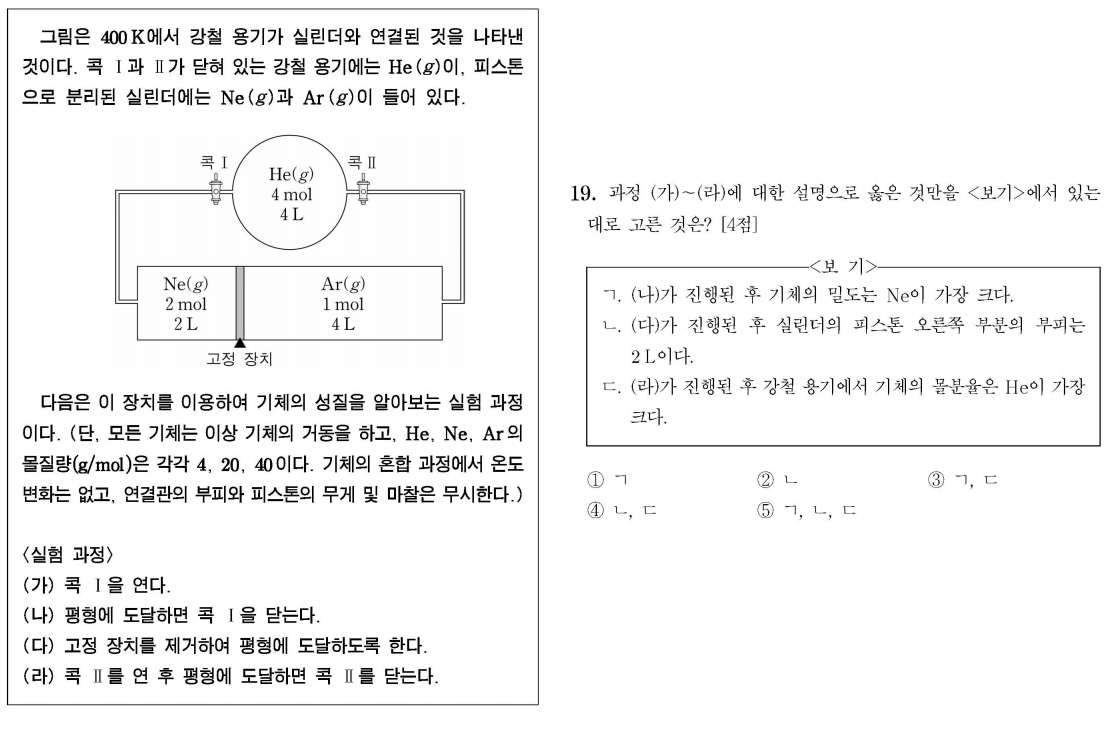

ㄱ. 콕 I을 열면 강철 용기와 피스톤 왼쪽 공간은 압력이 같으므로 몰수에 비례하여 분포하게 됩니다.
따라서 피스톤 왼쪽에 He 4/3 mol, Ne 2/3 mol이 위치하게 됩니다.
기체 밀도를 계산해보면 PV = WRT / M이므로, W/V = PM/RT 이고 이것은 PM에 비례합니다.
편의상 PV = n (RT = 1)으로 두면 He는 4/3 atm, Ne는 2/3 atm입니다.
밀도를 구해보면 Ne는 4/3 × 4, Ne는 2/3 × 20, Ar는 1/4 × 40입니다.
따라서 Ar의 밀도가 가장 큼을 알 수 있습니다.
ㄴ. 고정 장치 제거 시 왼쪽 기체는 4/3 + 2/3 = 2mol이고, 오른쪽 기체는 1mol이므로
몰수에 비례하여 왼쪽이 4L, 오른쪽이 2L이며 이 때 양쪽의 얍력은 1/2 atm임을 알 수 있습니다.
ㄷ. 콕 II를 열면 각 기체의 몰수는 He 8/3 mol, Ne 4/3 mol, Ar 1mol이므로 몰분율은 He가 가장 큽니다.
따라서 정답은 4번임을 알 수 있습니다.
2013학년도 21번


이러한 열량 계산 문제는 쉽지만 의외로 빨리 풀려다가 엉뚱한 데에서 틀릴 수가 있습니다.
ㄱ, ㄴ. 쉽게 해결이 가능합니다.
ㄷ. 상 변환 상태에서 △S = △H/T이므로, 기화 엔트로피와 용융 엔트로피 변화량을 구할 수 있습니다.
용융시 시간은 5min만 지났기 때문에 그래프를 조심하여 1/2 칸으로 대입하여 계산해주면, 엔트로피 변화량은 6배임을 알 수 있습니다.
따라서 정답은 5번입니다.
2013학년도 22번


ㄱ. 편의 상 PV = n (RT = 1)로 두면, CO2의 증기압은 일정하게 유지되므로 콕 A, B를 연 후 n_CO2 = 1atm × 5L = 5mol입니다.
n_He = 1atm × 2L = 2mol이므로 몰분율을 계산하면 2/7임을 알 수 있습니다.
ㄴ. 평형 II에서 P_tot = 5.1atm이지만, CO2(l)이 존재하기 위해서는 P_CO2 ≥ 5.1atm이어야 합니다.
P_tot = P_CO2 + P_He이므로 P_CO2 < 5.1atm이고, 따라서 평형 II에서는 CO2(l)이 존재하지 않음을 알 수 있습니다.
ㄷ. P_CO2가 1atm(증기압) 이상인지를 통해 CO2(s)의 존재 여부를 알 수 있습니다.
우선 평형 I에서 P_He = 2/5, 평형 II에서는 P_He = 2/5 × T_2/T_1입니다.
평형 II에서 P_CO2는 최소 5.1 - 2/5 × 217/195 > 4입니다.
평형 III에서의 P_CO2는 넉넉잡아 계산해도 4 × 195/217이므로 이것은 1atm보다 크고, 따라서 CO2(s)는 존재함을 예상할 수 있습니다.
따라서 정답은 3번입니다.
2013학년도 23번


이 문제는 5지선다 문제인데 정답률이 6%라는 특이한 통계를 봤습니다.
ㄱ. A에서 0.4mol이 소모, B는 0.2mol이 생성되었으므로 계수는 2A → B로 반응함을 알 수 있습니다.
반응 몰수를 적절히 적어 계산해보면 P점에서는 A와 B의 몰수가 같은 지점이므로 0.5 - 2x = x의 식이 나오고, 이를 풀어 x를 계산한 뒤 Q_P 값을 계산해보면 6임을 알 수 있습니다.
ㄴ. 정반응의 표준 깁스 자유에너지의 부호를 구하는 보기인데, 우선 K_C가 아닌 K_P를 구해야하므로 (RT)^△n_g 값을 구해주면 0.8이고, 이 때 K_P < 1이므로 표준 깁스 자유 에너지는 0보다 큼을 알 수 있습니다.
ㄷ. 농도 = n/V이므로 부피를 2배하면 농도는 1/2이 됩니다.
2A → B 반응식에서 몰수를 다시 작성하여 A를 0.1mol로 맞춰두고 Q값을 구해 K와 비교하여야 합니다.
따라서 생성물 농도를 보면 A는 0.1mol, B는 0.075mol이고 이를 통해 Q 값을 계산해보면 이는 K보다 작으므로, 정반응이 진행될 것임을 예상할 수 있습니다.
따라서 A의 농도는 0.1M에서 더 작아지므로 보기 ㄷ은 틀렸습니다.
따라서 정답은 1번입니다.
2013학년도 24번


시간에 따른 반응물 역수의 그래프를 보여주고 이에 대해 옳은 설명을 고르는 문제입니다.
ㄱ. T_1과 T_2일 때 일차 함수로 주어진 그래프 식을 작성하고, 이를 연립하여 t를 계산하면 P점에서의 t를 구할 수 있습니다.
ㄴ. 1/[A]이 시간에 대한 일차 함수로 나타나므로, 이 반응은 A에 대한 2차 반응임을 알 수 있습니다.
(이를 단번에 알기 위해서는 0차, 1차, 2차 반응 농도 식을 알아야 합니다.)
따라서 v = k[A]^2 꼴로 나타낼 수 있고, 그래프 개형을 통해 k 값의 비율과 1/[A]^2 값의 비율을 구해 v 값의 비율을 구하면 v_1 < v_2임을 알 수 있습니다.
ㄷ. ln k2/k1 = -E_a/R(1/T_2 - 1/T_1) (부호와 1, 2의 위치를 잘 기억해야 합니다.) 식을 이용하여 계산하면,
E_a가 보기 ㄷ에서 제시한 식이 맞음을 알 수 있습니다.
따라서 정답은 4번입니다.
2013학년도 25번


문제 난이도 자체는 어렵지 않으나 25번에 배치되어있어 시간이 넉넉하지 않다면 급하게 풀기 힘든 문제입니다.
ㄱ. 실험 상황이 약산을 강염기 KOH로 적정하는 상황이므로 당량점에서 용액은 염기성이 됩니다.
따라서 페놀프탈레인 지시약을 사용해 당량점 도달 여부를 확인해야 합니다.
ㄴ. 프탈산 10mmol 적정 때 KOH 10mL를 사용하였고, 질산 적정 때 KOH를 6mL 사용하였으므로 질산은 6mmol이 포함되어 있습니다.
밀도는 1.20g/mL이라고 하였으므로 1mL 질산은 1.20g입니다.
이를 이용해 % 농도를 계산하면 31.5%임을 알 수 있습니다.
ㄷ. 문제에서 프탈산 수소 구조를 제시해줬으므로 이를 통해 적정 알짜 이온 반응식을 쓸 수 있습니다.
따라서 정답은 1번입니다.
'자연과학(PEET) > 일반화학' 카테고리의 다른 글
| [PEET 일반화학] 2015학년도 5회 PEET 일반화학 고난도 기출문제 풀이/해설 (0) | 2021.07.21 |
|---|---|
| [PEET 일반화학] 2014학년도 4회 PEET 일반화학 고난도 기출문제 풀이/해설 (0) | 2021.07.19 |
| [PEET 일반화학] 2012학년도 2회 PEET 일반화학 고난도 기출문제 풀이/해설 (0) | 2021.07.17 |
| [PEET 일반화학] 2011학년도 1회 PEET 일반화학 고난도 기출문제 풀이/해설 (0) | 2021.07.17 |
| [PEET 일반화학] 2021학년도 11회 PEET 일반화학 고난도 기출문제 풀이/해설 (0) | 2021.07.08 |