복습 정리 노트

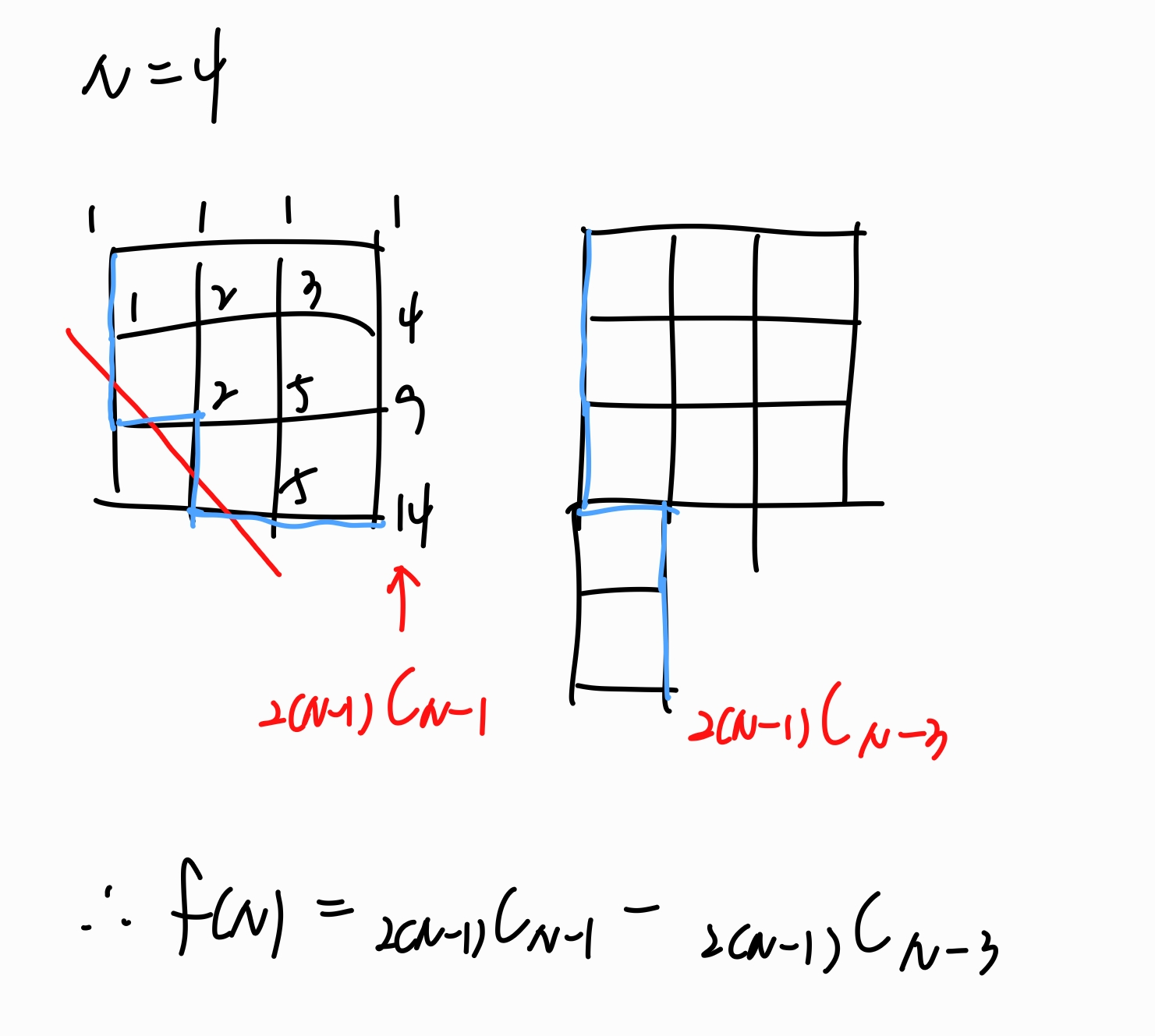
백준 BOJ 21739번 : 펭귄 네비게이터 문제 난이도 : Gold II 알고리즘 분류 : 조합론, DP 2 x N 격자에서 펭귄이 어떤 경로로 오른쪽과 아래로만 이동하더라도 더 큰 번호로만 이동하며 도착할 수 있도록 번호를 매긴다고 할 때 경우의 수를 구하는 문제이다. 높이가 2이므로 2부터 N-1까지 위쪽 또는 아래쪽 줄을 선택하면서 번호를 매길 수 있다. 규칙을 찾아보면 윗줄보다 아랫줄을 선택하는 순간이 2번 이상일 경우 조건에 어긋나게 된다. 따라서 이는 (0, 0)에서 (N, N)으로 격자를 따라 오른쪽과 아래로만 이동하는데, 아래를 오른쪽보다 2번 이상 선택하지 않는 경우의 수와 같고 이를 시각화하면 다음과 같다. 위는 N = 4일 때의 문제 상황을 앞서 설명한 다른 격자판으로 일대일 대응시..

백준 BOJ 4383번 : 점프는 즐거워 문제 난이도 : Silver V 알고리즘 분류 : 구현 길이 N인 수열이 주어질 때 인접한 N-1개의 정수 쌍에 대해 그 차이의 절댓값이 1 ~ N-1까지 모두 등장하는 수열인지 아닌지를 판별하는 문제이다. 간단한 구현 문제인데 정답률이 24%밖에 되지 않아 반례가 있나 싶었는데, 첫 제출에 간단하게 정답 처리를 받은 것으로 보아 EOF까지 입력받는 처리가 까다로워서 많은 사람들이 틀리지 않았나 싶다. #include #define int long long using namespace std; main() { ios_base::sync_with_stdio(false); cin.tie(NULL), cout.tie(NULL); int N; while(cin >> N)..

백준 BOJ 20162번 : 간식 파티 문제 난이도 : Silver II 알고리즘 분류 : DP 문제에 조건이 앞쪽에 숨겨져 있는데, 잘 보면 이전에 먹은 간식보다 점수가 높은 간식만 먹는다는 조건이 있다. 따라서 이 문제는 합이 가장 큰 증가하는 부분 수열 문제가 된다. 마지막에 답을 출력할 때 dp[N-1]이 아닌 모든 dp 값 중 최댓값을 출력해야 함에 유의하자. #include #define int long long using namespace std; main() { ios_base::sync_with_stdio(false); cin.tie(NULL), cout.tie(NULL); int N; cin >> N; vector v(N); for(int i=0; i> v[i]; vector dp(v)..

백준 BOJ 9764번 : 서로 다른 자연수의 합 문제 난이도 : Silver I 알고리즘 분류 : DP 자연수 N을 서로 다른 자연수들의 합으로 나타내는 방법의 수를 구하는 문제이다. 아주 아주 기초적인 DP 문제임에도 점화식을 못 떠올려서 꽤 오래 막혔고, 풀이를 참고했다. 점화식은 다양한 방법으로 세울 수 있겠으나, 참고한 풀이는 "dp(a, b) : b 이하의 수들의 합으로 a를 만드는 경우의 수"와 같이 dp를 정의하는 것이다. 그렇게 한다면 b를 증가시켜 가면서 dp(a, b) = dp(a-b, b+1) + dp(a, b+1) (즉, b를 a의 합에 넣어주는 경우와 그렇지 않은 경우의 합) 탑다운 방식으로 답을 구해줄 수 있다. 처리해야 할 예외는 다음과 같다. 1. dp 값이 이미 구해진 경..

2022년 7월 12일 화요일 푼 문제들과 사용되는 개념들을 정리한다. 백준 BOJ 1615번 : 교차 개수 세기 문제 난이도 : Gold I 알고리즘 분류 : 세그먼트 트리 N개의 점들의 쌍에 대해 M개의 선분이 주어질 때 교차 개수를 세는 문제이다. 세그먼트 트리의 가장 대표적인 문제들 중 하나인 Inversion Counting Problem인데 왜 그동안 못 풀고 있었나 봤더니 점들의 위치가 중복되어 주어진다는 점 때문이었다. 생각해보니 기존의 Inversion Counting Problem에서 같은 점이 주어져도 update 함수에서 tree[node] = 1로 설정해주었는데, 해당 노드에 점이 하나 추가되는 것이므로 간단히 tree[node]++와 같이 값을 갱신해주기만 하면 되는 문제였다. ..

2차원 배열에서 특정 직사각형 구간을 잡아 얻을 수 있는 구간의 최대 합을 가장 빠른 시간에 구할 수 있는 알고리즘은 무엇일까요? 특정한 점화식을 사용하는 세그먼트 트리를 이용하면 2차원 공간에서의 최대 구간합을 O(N^2 log N)에 구할 수 있다는 것이 잘 알려져 있으며, 이 알고리즘을 사용하는 문제가 정보 올림피아드에 '금광'이라는 이름의 문제로 출제되어 많은 사람들이 이를 금광 세그라고 부릅니다. 이 포스트에서는 금광 세그에 대해 공부한 것을 간단하게 설명해보고, 이를 구현해볼 것입니다. 백준 BOJ 10167번 : 금광 N개의 점이 주어지고, 각 점에 대해 x, y 좌표와 가중치 w가 주어질 때, 특정 직사각형 형태의 구간을 잡아 얻을 수 있는 최대 구간 합을 구하는 문제입니다. 풀이 코드가 ..

알고리즘에 대한 글을 작성하면 일반적으로 하나의 주제를 잡고 정리해야 하는데, 글 하나에 정리할 정도로 내용이 많지 않은 작은 테크닉이나 단일 문제들의 경우 포스트 하나마다 따로 작성하기가 용이하지 않기 때문에, 이 카테고리에 큰 형식의 틀 없이 모아서 작성해보려고 한다. 백준 BOJ 10986번 : 나머지 합 N개의 수로 이루어진 수열에 대해 연속된 구간의 합이 M으로 나누어 떨어지는 구간의 수를 구하는 문제이다. (1 ≤ N ≤ 10^6) 가장 먼저 떠오르는 풀이는 누적 합을 이용해서 O(N^2)에 푸는 건데, 그렇게 할 경우 당연히 시간 초과이다. i ~ j번째 구간의 합이 M으로 나눈 나머지가 0이라는 것과 동치는 무엇일까? 누적 합을 이용하여 생각해보면, 1 ~ j번째 구간 합에서 1 ~ (i-..

vector, string 내에서 인접한 값끼리 비교할 때 for(int i=1; i

백준 BOJ 14958번 : Rock Paper Scissors 문제 난이도 : Diamond V 알고리즘 분류 : FFT (고속 푸리에 변환) 배열이 2개가 주어지고, 각각의 배열의 값들이 가위바위보에 해당하는 Rock, Paper, Scissors라고 할 때, 아래의 배열이 이동하면서 매칭되는 칸끼리 가위바위보를 수행하여 위치에 따라 가장 많이 이길 수 있는 횟수를 구하는 문제입니다. 이 문제의 상황과 같이 배열과 배열을 일대일로 비교를 여러 번 해야하는 경우 FFT를 활용해볼 수 있습니다. 한 쪽의 벡터를 뒤집은 뒤 이산 합성곱을 수행해주면 항마다 일대일로 매칭되어 곱해진 값이 더해지므로, 이를 활용하기 위해 적절히 벡터의 값을 1 또는 0으로 세팅해주어야 합니다. 문제 상황에 대해 생각해보면 N칸..

백준 BOJ 13055번 : K-Inversions 문제 난이도 : Diamond V 알고리즘 분류 : FFT (고속 푸리에 변환) B가 A보다 먼저 나오는 쌍을 inversion이라고 할 때, B와 A 사이의 거리가 K일 때 그 쌍을 K-Inversion이라고 정의합시다. A와 B로만 이루어진 문자열에 대해 0 ~ N-1사이의 모든 K-inversion의 수를 구하는 문제입니다. 예를 들어 문제에서 예시로 든 BABA를 가지고 설명하자면, 앞의 BA와 뒤의 BA는 모두 B → A 순서대로 나타나며 B와 A 사이의 거리가 1이므로 1-inversion이고, 이는 총 2회 나옵니다. 그리고 맨 앞의 B와 맨 뒤의 A 역시 inversion에 해당되고, 두 문자 사이의 거리는 3이므로 3-inversion은..