백준 BOJ 14958번 : Rock Paper Scissors
문제 난이도 : Diamond V
알고리즘 분류 : FFT (고속 푸리에 변환)

배열이 2개가 주어지고, 각각의 배열의 값들이 가위바위보에 해당하는 Rock, Paper, Scissors라고 할 때, 아래의 배열이 이동하면서 매칭되는 칸끼리 가위바위보를 수행하여 위치에 따라 가장 많이 이길 수 있는 횟수를 구하는 문제입니다.
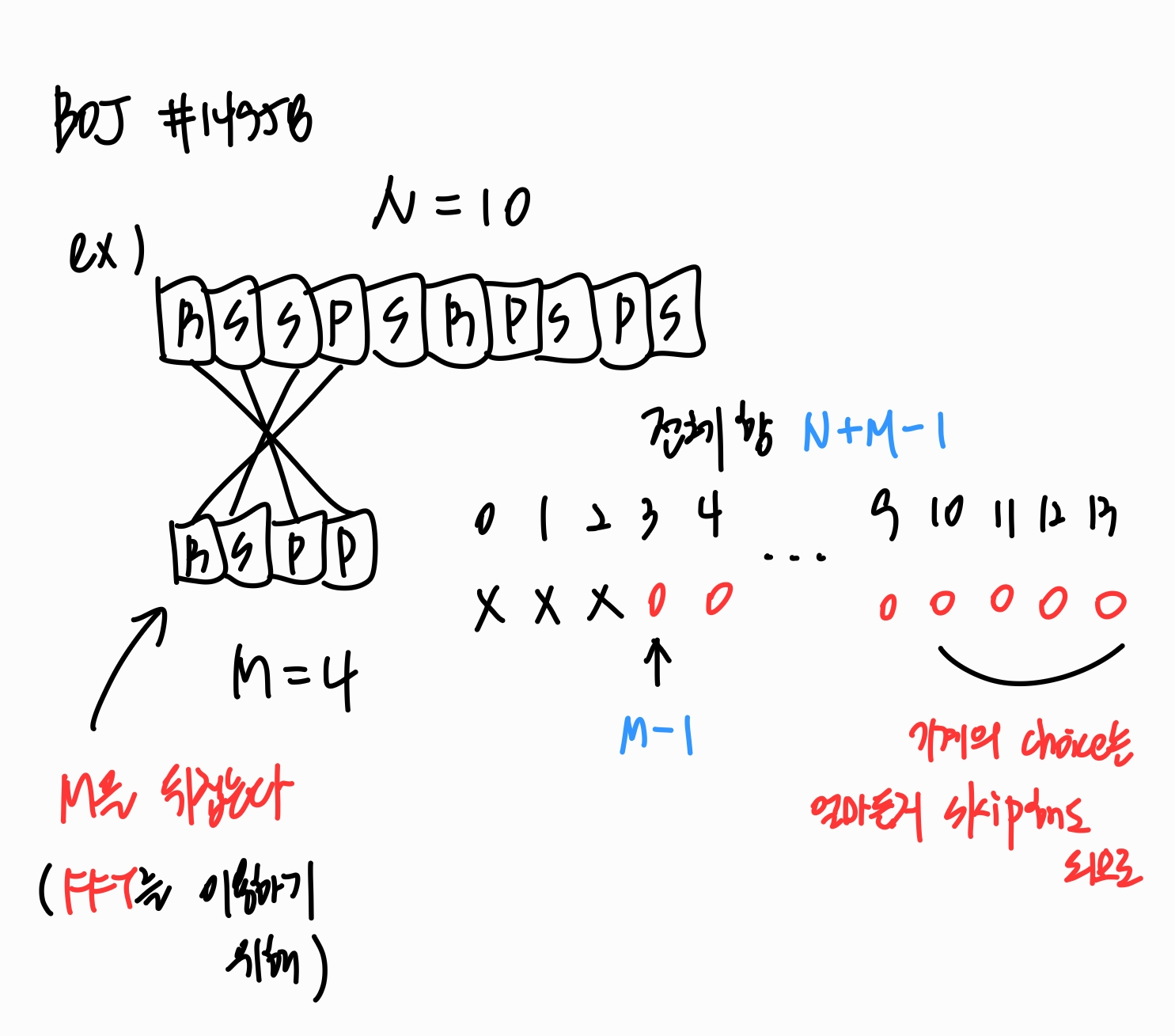
이 문제의 상황과 같이 배열과 배열을 일대일로 비교를 여러 번 해야하는 경우 FFT를 활용해볼 수 있습니다.
한 쪽의 벡터를 뒤집은 뒤 이산 합성곱을 수행해주면 항마다 일대일로 매칭되어 곱해진 값이 더해지므로, 이를 활용하기 위해 적절히 벡터의 값을 1 또는 0으로 세팅해주어야 합니다.
문제 상황에 대해 생각해보면 N칸의 배열에 대해 M칸의 배열을 평행이동 시키며 확인하는 상황이고, 위의 그림과 같이 왼쪽 끝을 맞춘 상태부터 시작하여 오른쪽으로 평행이동하면 됩니다.
전체 항의 수는 N+M-1개가 나오게 되고, 기계의 choice는 얼마든지 skip해도 되므로 M-1번째 항부터 마지막 항(N+M-1번째 항)까지가 고려해주어야 하는 범위임을 알 수 있습니다.
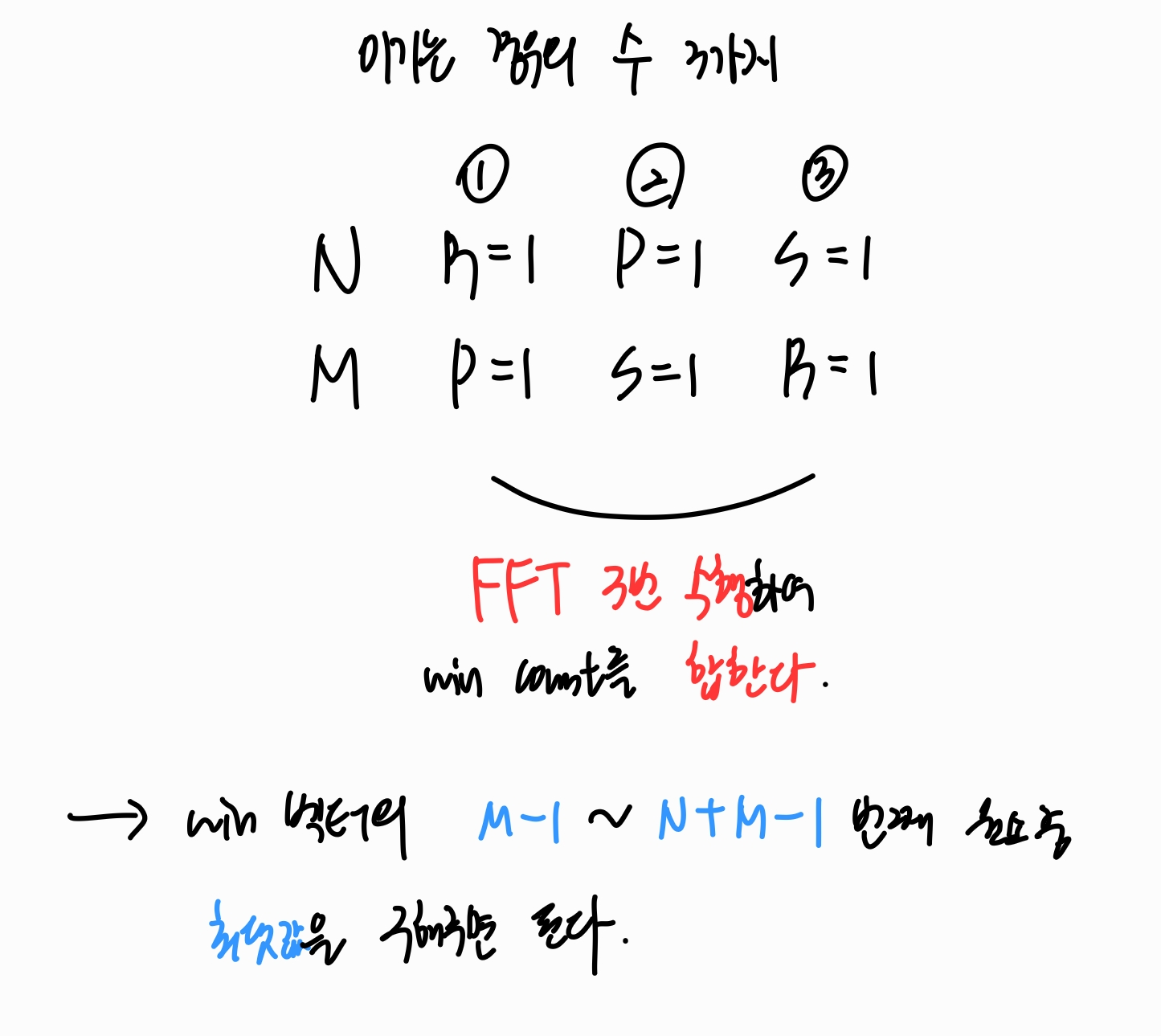
그렇다면 곱할 벡터의 값을 어떻게 세팅해주어야 할까요?
가위바위보에서 이기는 경우의 수는 위와 같이 3가지입니다.
우리가 설정할 수 있는 값은 0과 1뿐이므로, 그냥 세 가지 상황에 대해 세 번의 다른 세팅을 해주면 됩니다.
예를 들어 위의 벡터에 대해서는 R = 1, 아래에 대해서는 P = 1로 세팅 후 FFT를 돌려주고, 종합할 벡터에 값을 옮겨주고, 다시 벡터를 세팅해주고 하는 과정을 반복하는 것입니다.
최종적으로 합친 값들에서, 벡터의 M-1 ~ N+M-1번째 원소 중에서 최댓값이 답이 됩니다.
#include <bits/stdc++.h>
#define int long long
using namespace std;
const double PI = acos(-1);
typedef complex<double> cpx;
void FFT(vector<cpx> &v, bool inv) {
int S = v.size();
for(int i=1, j=0; i<S; i++) {
int bit = S/2;
while(j >= bit) {
j -= bit;
bit /= 2;
}
j += bit;
if(i < j) swap(v[i], v[j]);
}
for(int k=1; k<S; k*=2) {
double angle = (inv ? PI/k : -PI/k);
cpx w(cos(angle), sin(angle));
for(int i=0; i<S; i+=k*2) {
cpx z(1, 0);
for(int j=0; j<k; j++) {
cpx even = v[i+j];
cpx odd = v[i+j+k];
v[i+j] = even + z*odd;
v[i+j+k] = even - z*odd;
z *= w;
}
}
}
if(inv)
for(int i=0; i<S; i++) v[i] /= S;
}
vector<int> mul(vector<int> &v, vector<int> &u) {
vector<cpx> vc(v.begin(), v.end());
vector<cpx> uc(u.begin(), u.end());
int S = 2;
while(S < v.size() + u.size()) S *= 2;
vc.resize(S); FFT(vc, false);
uc.resize(S); FFT(uc, false);
for(int i=0; i<S; i++) vc[i] *= uc[i];
FFT(vc, true);
vector<int> w(S);
for(int i=0; i<S; i++) w[i] = round(vc[i].real());
return w;
}
main() {
ios_base::sync_with_stdio(false);
cin.tie(NULL), cout.tie(NULL);
int N, M; cin >> N >> M;
string a, b; cin >> a >> b;
reverse(b.begin(), b.end());
vector<int> v(N), u(M), win(N+M-1);
for(int i=0; i<N; i++) {
if(a[i] == 'R') v[i] = 1;
else v[i] = 0;
}
for(int i=0; i<M; i++) {
if(b[i] == 'P') u[i] = 1;
else u[i] = 0;
}
vector<int> w = mul(v, u);
for(int i=0; i<N+M-1; i++) win[i] += w[i];
for(int i=0; i<N; i++) {
if(a[i] == 'P') v[i] = 1;
else v[i] = 0;
}
for(int i=0; i<M; i++) {
if(b[i] == 'S') u[i] = 1;
else u[i] = 0;
}
w = mul(v, u);
for(int i=0; i<N+M-1; i++) win[i] += w[i];
for(int i=0; i<N; i++) {
if(a[i] == 'S') v[i] = 1;
else v[i] = 0;
}
for(int i=0; i<M; i++) {
if(b[i] == 'R') u[i] = 1;
else u[i] = 0;
}
w = mul(v, u);
for(int i=0; i<N+M-1; i++) win[i] += w[i];
int ans = 0;
for(int i=M-1; i<N+M-1; i++) ans = max(ans, win[i]);
cout << ans << "\n";
}
구현 자체는 일반 FFT + 위에서 언급한 벡터 초기화 3번 정도만 구현해주면 되므로 크게 어렵지 않습니다.
위의 코드에서는 win 벡터에 최종적으로 합칠 값들이 더해집니다.
M-1 ~ N-1이 아닌 M-1 ~ N+M-1까지 검사해주어야 함에 조심합시다.
(문제에서 주어지는 테스트케이스 중 예제 4를 넣어봄으로써 확인할 수 있습니다.)
+ Solved.ac Diamond IV 티어 달성!

'알고리즘 > 백준(BOJ) 문제풀이' 카테고리의 다른 글
| 백준 BOJ 최대 유량 알고리즘 문제 다시 풀어보기 (Network Flow) (0) | 2022.07.27 |
|---|---|
| [백준 BOJ 알고리즘] 수열에서 a_j - a_i = a_k - a_j인 i < j < k 구하기 (3) | 2022.07.21 |
| 백준 BOJ 13055번 : K-Inversions 풀이 (FFT, 고속 푸리에 변환) (0) | 2022.06.29 |
| 백준 BOJ 13575번 : 보석 가게 풀이 (FFT, 고속 푸리에 변환) (0) | 2022.06.29 |
| 백준 BOJ 13279번 : 곱의 합 쿼리 풀이 (FFT, 고속 푸리에 변환) (0) | 2022.06.28 |