반응형
백준 BOJ 16975번 : 수열과 쿼리 21
16975번: 수열과 쿼리 21
길이가 N인 수열 A1, A2, ..., AN이 주어진다. 이때, 다음 쿼리를 수행하는 프로그램을 작성하시오. 1 i j k: Ai, Ai+1, ..., Aj에 k를 더한다. 2 x: Ax 를 출력한다.
www.acmicpc.net
문제 난이도 : Platinum IV
알고리즘 분류 : 느리게 갱신되는 세그먼트 트리 (Lazy Propagation of Segment Tree)
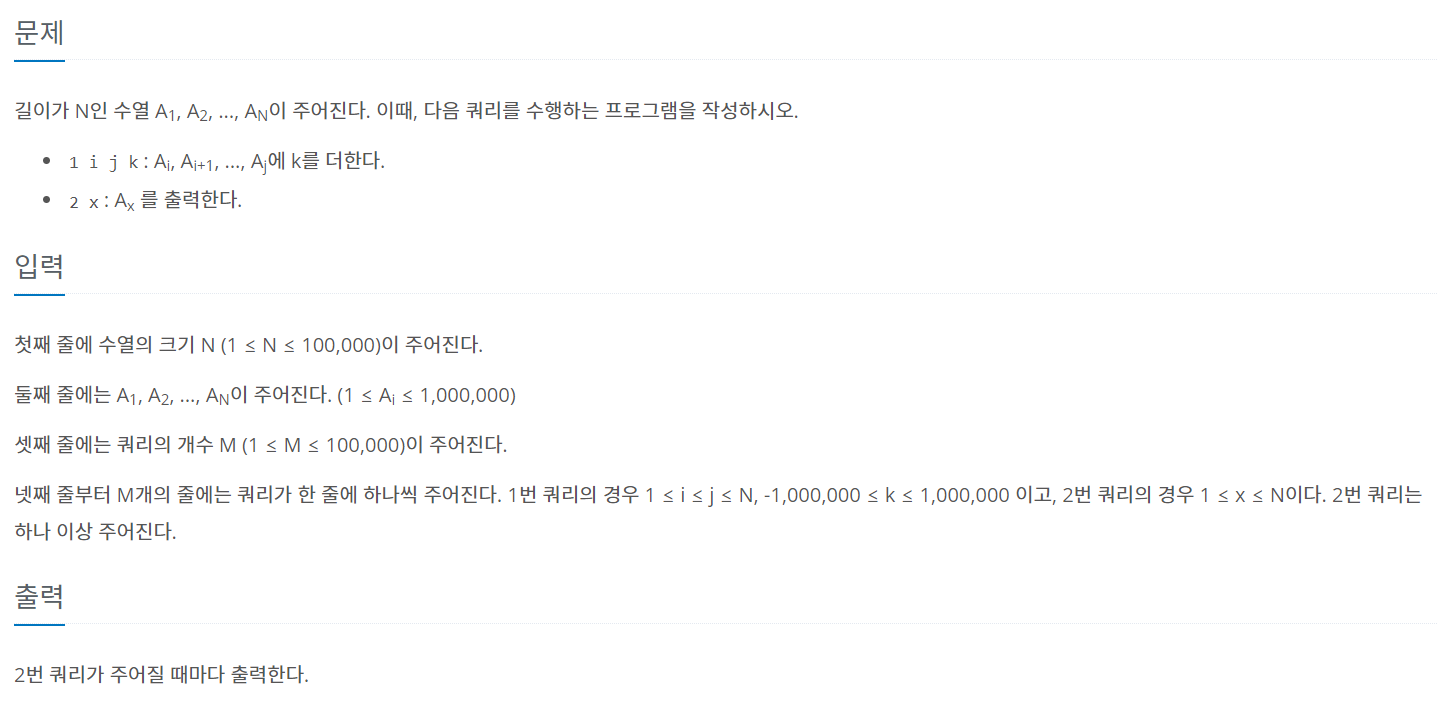
1번 쿼리에 대해서는 구간의 모든 원소에 특정 값을 더해주고, 2번 쿼리에 대해서는 특정 주소의 원소를 출력해야한다고 할 때 최대 10만개의 쿼리를 처리하는 문제입니다.
(참고로 이 문제는 1번 쿼리는 구간 쿼리이지만 2번 쿼리는 구간에 대한 쿼리가 아니므로 일반 세그먼트 트리로도 풀 수 있는 것으로 알고 있습니다.)
이 포스트에서는 구간 연산이 편리한 Lazy Propagation으로 풀이해보도록 하겠습니다.
#include <bits/stdc++.h>
#define int long long
using namespace std;
vector<int> v, u, w; // v : array, u : tree, w : lazy
int init(int n, int b, int e) {
if(b == e) return u[n] = v[b];
int lv = init(n*2, b, (b+e)/2);
int rv = init(n*2 + 1, (b+e)/2 + 1, e);
return u[n] = lv + rv;
}
void lazy(int n, int b, int e) {
if(w[n] == 0) return;
u[n] += (e-b+1)*w[n];
if(b != e) {
w[n*2] += w[n];
w[n*2 + 1] += w[n];
}
w[n] = 0;
}
int upd(int n, int b, int e, int l, int r, int add) {
lazy(n, b, e);
if(r < b || e < l) return u[n];
if(l <= b && e <= r) {
w[n] += add;
lazy(n, b, e);
return u[n];
}
int lv = upd(n*2, b, (b+e)/2, l, r, add);
int rv = upd(n*2 + 1, (b+e)/2 + 1, e, l, r, add);
return u[n] = lv + rv;
}
int query(int n, int b, int e, int idx) {
lazy(n, b, e);
if(b == e) return u[n];
if(idx <= (b+e)/2) return query(n*2, b, (b+e)/2, idx);
else return query(n*2 + 1, (b+e)/2 + 1, e, idx);
}
main() {
ios_base::sync_with_stdio(false);
cin.tie(NULL), cout.tie(NULL);
int N; cin >> N;
v.resize(N+1);
for(int i=1; i<=N; i++) cin >> v[i];
u.resize(N*4);
init(1, 1, N);
w.resize(N*4);
int M; cin >> M;
while(M--) {
int Q; cin >> Q;
if(Q == 1) {
int a, b, c; cin >> a >> b >> c;
upd(1, 1, N, a, b, c);
}
else if(Q == 2) {
int a; cin >> a;
cout << query(1, 1, N, a) << "\n";
}
}
}
1번 쿼리의 경우에는 일반적인 '느리게 갱신되는 세그먼트 트리'를 활용하여 위와 같이 풀이할 수 있습니다.
2번 쿼리는 하나의 원소만을 출력해주면 되므로, 트리에서 값의 주소에 따라 왼쪽 및 오른쪽으로 이동해 내려가면서 특정 주소의 원소 하나에 해당하는 리프 노드에 도달할 때까지 이동한 뒤 재귀적으로 값을 얻어와 출력해주면 됩니다. (이는 일반 세그먼트 트리에서도 다루었던 내용입니다.)

반응형
'알고리즘 > 백준(BOJ) 문제풀이' 카테고리의 다른 글
| 백준 BOJ 2934번 : LRH 식물 (느리게 갱신되는 세그먼트 트리) (0) | 2022.06.25 |
|---|---|
| BOJ 12844 XOR, BOJ 14245 XOR, BOJ 11962 Counting Haybales (느리게 갱신되는 세그먼트 트리) (0) | 2022.06.24 |
| 백준 BOJ 1395번 : 스위치 (느리게 갱신되는 세그먼트 트리, Lazy Propagation) (0) | 2022.06.23 |
| 백준(BOJ) 런타임 전의 전처리 + 구성적 문제 풀이 예제 (BOJ 22223) (0) | 2022.06.21 |
| 백준 수열과 쿼리 18 (BOJ 14504), 수열과 쿼리 1.5 (BOJ 17410) 풀이 (제곱근 분할법) (5) | 2022.06.12 |