백준에서 나름 재미있게 푼 문제가 있어서 정리해봅니다.
"런타임 전의 전처리"와 "구성적" 태그가 둘 다 달려있는 문제였는데, 각 태그는 다음과 같은 조건에 의해 분류됩니다.
런타임 전의 전처리 : 제출한 프로그램이 작동하면서 문제를 푸는 것 외에, 풀이를 얻기 위해 미리 다른 프로그램을 작성하여 계산하는 방식으로 다른 전략을 취하여 푸는 문제입니다.
15698번: Uncrossed Knight’s Tour
A well-known puzzle is to “tour” all the squares of an 8 × 8 chessboard using a knight, which is a piece that can move only by jumping one square in one direction and two squares in an orthogonal direction. The knight must visit every square of the ch
www.acmicpc.net
극단적으로는 위와 같은 문제가 있습니다.
(ACM-ICPC World Finals 문제이며 난이도는 무려 루비2입니다.)
구성적 : 문제에서 제시한 조건을 충족하는 아무 답이나 제출하면 정답 처리를 받을 수 있는 문제입니다.
이 둘을 적절히 활용해야 하는 문제를 풀이해봅시다.
백준 BOJ 22223번 : Table 2

위의 조건을 만족하는 M = 13인 Table을 구하여 아무거나 출력하는 문제입니다.
일단 Text 제출이므로, 저의 경우에는 한 가지 꼼수를 썼습니다.
바로 정답자의 코드 길이를 확인하는 것인데요, 확인해보면 다음과 같습니다.
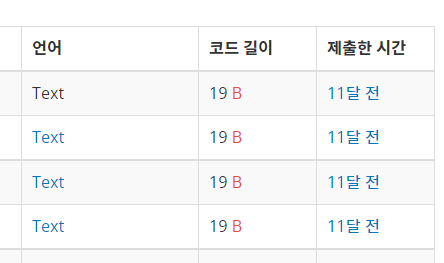
정답자의 제출 코드 길이가 19B라면, 첫 줄에 N과 개행 문자가 들어가고, 그 다음 N*N의 표가 나옴을 이용하여 간단히 계산해보면 N = 3임을 알 수 있습니다.
따라서 N = 3인 모든 Table에 대해서 조건을 만족하는 경우를 찾아보면 됩니다.
#include <bits/stdc++.h>
#define int long long
using namespace std;
main() {
ios_base::sync_with_stdio(false);
cin.tie(NULL), cout.tie(NULL);
for(int i1=1; i1<=9; i1++)
for(int i2=1; i2<=9; i2++)
for(int i3=1; i3<=9; i3++)
for(int i4=1; i4<=9; i4++)
for(int i5=0; i5<=9; i5++)
for(int i6=0; i6<=9; i6++)
for(int i7=1; i7<=9; i7++)
for(int i8=0; i8<=9; i8++)
for(int i9=0; i9<=9; i9++) {
bool check = true;
if((i1*100 + i2*10 + i3) % 13 != 0) check = false;
if((i4*100 + i5*10 + i6) % 13 != 0) check = false;
if((i7*100 + i8*10 + i9) % 13 != 0) check = false;
if((i1*100 + i4*10 + i7) % 13 != 0) check = false;
if((i2*100 + i5*10 + i8) % 13 != 0) check = false;
if((i3*100 + i6*10 + i9) % 13 != 0) check = false;
if((i1*100 + i5*10 + i9) % 13 != 0) check = false;
if((i3*100 + i5*10 + i7) % 13 != 0) check = false;
if(check) {
cout << i1 << " " << i2 << " " << i3 << "\n";
cout << i4 << " " << i5 << " " << i6 << "\n";
cout << i7 << " " << i8 << " " << i9 << "\n";
cout << "\n";
}
}
}
위와 같이 9개 정수에 대해 수의 범위만 만족하도록 하여, 모든 줄과 대각선이 13의 배수인 경우 표를 출력하도록 구현하였습니다.

코드를 돌려보면 위와 같이 수의 범위를 만족하는 모든 Table들이 구해집니다.
저 중에서 모든 행과 열, 대각선에 해당하는 세 자릿수 중에서 중복되는 쌍이 없는 Table은 빨간색 표시를 한 Table이 유일합니다.
따라서 다음과 같은 정답을 제출해주면 됩니다.
3
6 2 4
1 8 2
1 6 9
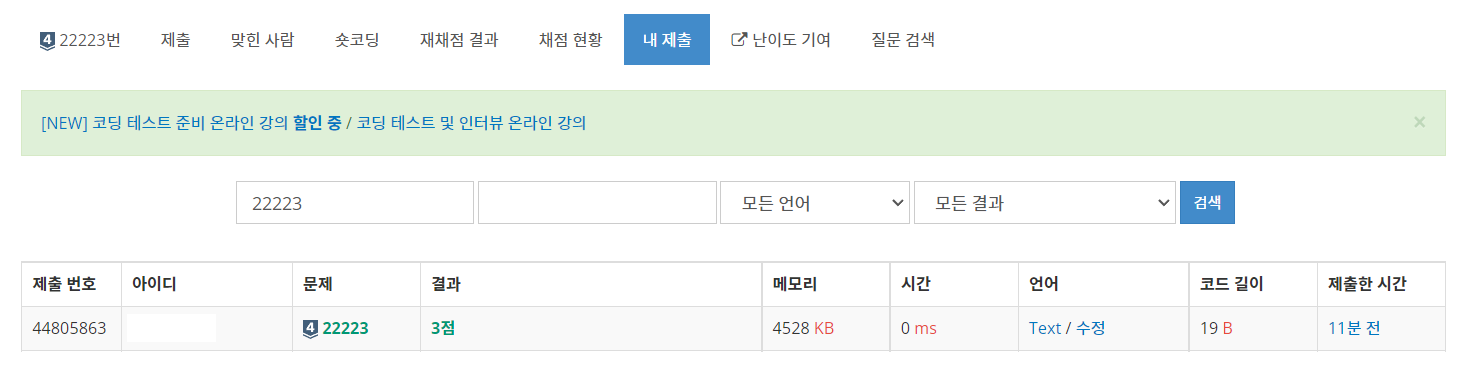
위와 같이 정답 처리를 받을 수 있습니다.
'알고리즘 > 백준(BOJ) 문제풀이' 카테고리의 다른 글
| 백준 BOJ 16975번 : 수열과 쿼리 21 (느리게 갱신되는 세그먼트 트리, Lazy Propagation) (0) | 2022.06.23 |
|---|---|
| 백준 BOJ 1395번 : 스위치 (느리게 갱신되는 세그먼트 트리, Lazy Propagation) (0) | 2022.06.23 |
| 백준 수열과 쿼리 18 (BOJ 14504), 수열과 쿼리 1.5 (BOJ 17410) 풀이 (제곱근 분할법) (5) | 2022.06.12 |
| [PS/BOJ] 프로그래밍에서 인터랙티브 문제 푸는 법 (예제 풀이 포함) (0) | 2022.06.01 |
| BOJ 2098 외판원 순회 (비트필드를 이용한 다이나믹 프로그래밍) (0) | 2022.04.27 |