이 포스트에서는 프로그래밍 문제 사이트 백준 Online Judge(BOJ)의 2981번 : '검문', 3036번 : '링' 문제의 풀이 코드와 해설을 다루고 있습니다.
문제 난이도는 Solved.ac 기준 Silver ~ Gold 티어에 해당하며, 문제를 풀이하기 위해 정수론 및 조합론에 대한 배경 지식이 있으면 좋습니다.
2981번 : 검문
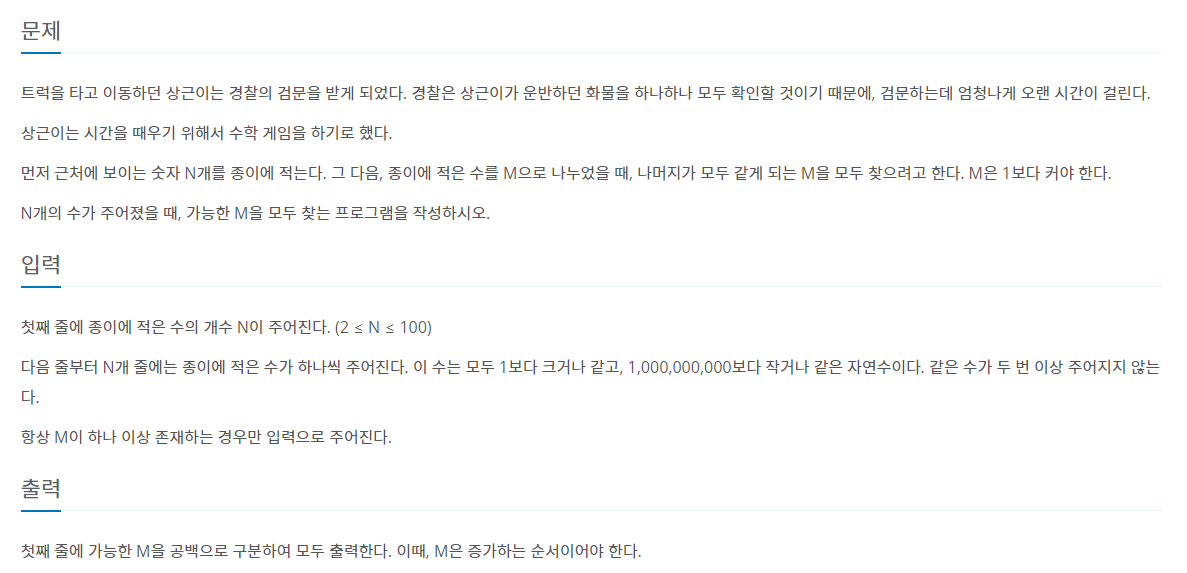
N개의 수를 M으로 나누었을 때 나머지가 모두 같도록 하는 M들을 오름차순으로 출력하는 문제입니다.
모든 M에 대한 나머지를 일일이 구해보는 방법도 있겠지만 이 문제에서는 N이 10억 이하이므로 그렇게 되면 시간 초과에 걸리게 됩니다.
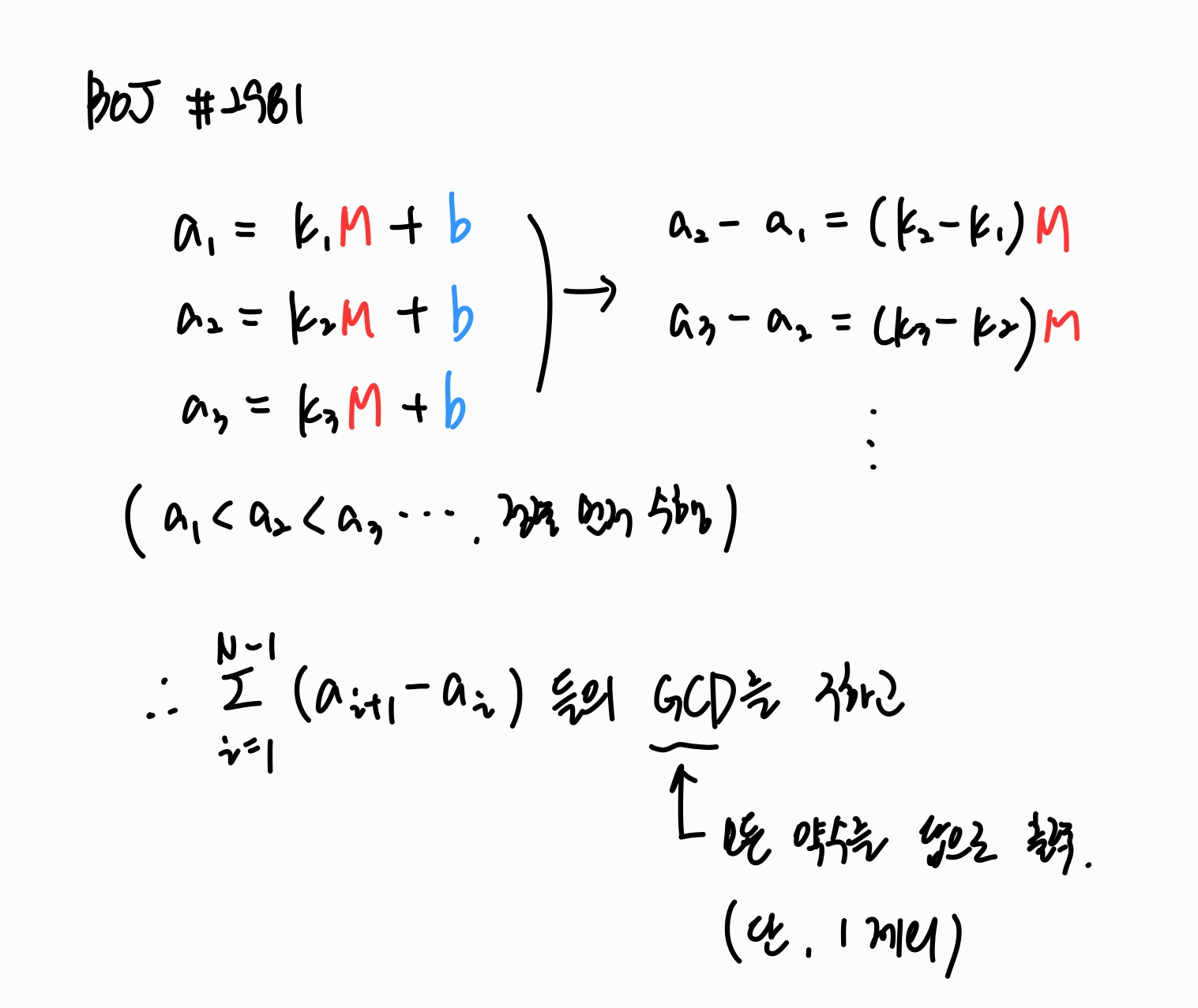
같은 나머지에 해당하는 b를 없애기 위해 수식을 조작하여 두 식을 빼보면, b를 없앨 수 있고 이 과정에서 공약수 M만이 남게 됩니다.
따라서 임의의 두 수들의 차이를 구하고 이들의 최대공약수를 구한 뒤, 그 GCD의 1을 제외한 모든 약수들을 정렬하여 출력해주면 되는 문제입니다. (여기서 임의의 두 수의 차이란 모든 쌍이 아닌 모든 수들이 한 번 이상 참여하기만 하면 됩니다. 따라서 굳이 a_i+1 - a_i로 구해줄 필요는 없음)
#include <bits/stdc++.h>
using namespace std;
int GCD(int a, int b) {
if(a < b) swap(a, b);
while(b != 0) {
int temp = a%b;
a = b;
b = temp;
}
return a;
}
int main() {
ios_base::sync_with_stdio(false);
cin.tie(NULL), cout.tie(NULL);
int N; cin >> N;
vector<int> arr(N);
for(int i=0; i<N; i++) cin >> arr[i];
sort(arr.begin(), arr.end());
int gcd = arr[1] - arr[0];
for(int i=2; i<N; i++)
gcd = GCD(gcd, arr[i] - arr[i-1]);
vector<int> ans;
for(int i=1; i*i<=gcd; i++)
if(gcd%i == 0) {
ans.push_back(i);
if(gcd/i != i) ans.push_back(gcd/i);
}
sort(ans.begin(), ans.end());
for(int i=1; i<ans.size(); i++)
cout << ans[i] << " ";
}
GCD를 계산하는 부분에서는 유클리드 호제법을 사용해야 시간 초과를 피할 수 있습니다.
GCD의 약수들을 구하는 부분에서는 i*i <= gcd로 잡고, 약수인 i를 구한 뒤 gcd/i 역시 약수이므로 ans에 저장해주는 방식을 사용하여 연산 시간을 줄였습니다.
3036번 : 링

인접한 링들이 반지름에 따라 몇 바퀴를 도는지 그 회전수 비를 출력하는 문제입니다.
둘레와 회전 수는 반비례하므로 이를 이용하여 기약분수를 구해서 출력해주면 됩니다.
다만 기약분수를 구하는 과정에서 유클리드 호제법을 사용해야 시간을 크게 단축시킬 수 있습니다.
#include <bits/stdc++.h>
using namespace std;
int GCD(int a, int b) {
if(a < b) swap(a, b);
while(b != 0) {
int temp = a%b;
a = b;
b = temp;
}
return a;
}
int main() {
ios_base::sync_with_stdio(false);
cin.tie(NULL), cout.tie(NULL);
int N, arr[100]; cin >> N;
for(int i=0; i<N; i++) cin >> arr[i];
for(int i=1; i<N; i++) {
int gcd = GCD(arr[0], arr[i]);
cout << arr[0]/gcd << "/" << arr[i]/gcd << "\n";
}
}
위와 같이 간단하게 구현해볼 수 있습니다.
'알고리즘 > 백준(BOJ) 문제풀이' 카테고리의 다른 글
| [백준/BOJ] 4949번 : 균형잡힌 세상, 17298번 : 오큰수 (스택) (0) | 2022.02.25 |
|---|---|
| [백준/BOJ] 11051번 : 이항 계수 2, 9375번 : 패션왕 신해빈, 2004번 : 조합 0의 개수 (조합, 경우의 수) (0) | 2022.02.25 |
| [백준/BOJ] 1019번 : 책 페이지 (수학, Counting) (+ Class 6 획득) (2) | 2022.02.24 |
| [백준/BOJ] 17371번 : 이사 (그리디 알고리즘, 기하학) (0) | 2022.02.24 |
| [백준/BOJ] 16565번 : N포커 (DP, 조합론, 포함과 배제의 원리) (0) | 2022.02.23 |