이 포스트에서는 프로그래밍 문제 사이트 백준 Online Judge(BOJ)의 1019번 : '책 페이지' 문제의 풀이 코드와 해설을 다루고 있습니다.
문제 난이도는 Solved.ac 기준 Gold I에 해당하며, 문제를 풀이하기 위해 수학에 대한 기본 지식이 있으면 좋습니다.
1019번 : 책 페이지
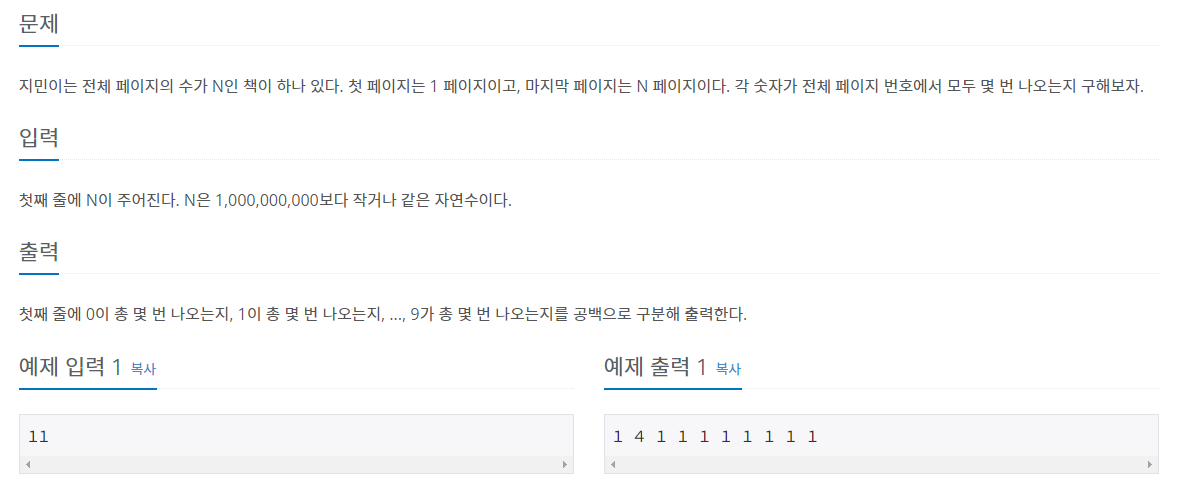
1부터 N까지의 수들 중에서 각 자릿수에 나오는 0~9들의 개수를 구하는 문제입니다.
단순히 counting을 해주면 N의 범위가 10억 이하이기 때문에 시간초과가 발생하므로, 빠르게 계산해줄 수 있는 공식을 구해서 풀이해주어야 합니다.

이런 Counting 문제는 과정을 결국 그려서 생각해보아야 하기 때문에 어쩔 수 없이 위와 같이 적어보았습니다.
예를 들어 N = 283이라고 가정하고 생각해보겠습니다.
그러면 일단 0 ~ 2는 일의 자리에 28번씩 등장하게 되고, 이것은 N/10의 값에 해당합니다.
4 ~ 9는 일의 자리에 28 + 1번씩 등장하게 되고, 이것은 N/10 + 1의 값에 해당합니다.
3의 경우에는 아직은 28번 등장하는데, 다음 턴에서부터 Counting 기준이 달라집니다.
이번에는 10으로 나눈 뒤 원래 10의 자리에 위치했던 수들의 개수를 세봅시다.
0 ~ 7은 총 (2+1)×10회 등장함을 알 수 있고, 9는 2×10회 등장함을 알 수 있습니다.
그런데 8의 경우에는 280, 281, 282, 283의 4개의 숫자가 더 등장하므로 이들을 고려해서 추가로 Count 해주어야 합니다.
이제 이 과정을 N > 0인 조건 하에서 N을 10으로 계속 나눠주면서 반복하면 됩니다.
위의 설명을 이제 코드로 구현해보겠습니다.
#include <bits/stdc++.h>
using namespace std;
int main() {
ios_base::sync_with_stdio(false);
cin.tie(NULL), cout.tie(NULL);
int N, cnt[10] = {}, add = 0;
cin >> N;
for(int i=1; N!=0; i*=10) {
int curr = N%10;
N /= 10;
cnt[0] -= i;
for(int j=0; j<curr; j++) cnt[j] += (N+1)*i;
cnt[curr] += N*i + 1 + add;
for(int j=curr+1; j<=9; j++) cnt[j] += N*i;
add += curr*i;
}
for(int i=0; i<=9; i++) cout << cnt[i] << " ";
}
먼저 현재 수의 마지막 자리를 N%10으로 구해주고, 이를 기준으로 좌우를 나누어 수를 다르게 Counting 해줄 것입니다.
그리고 연산을 간단하게 하기 위해 N은 미리 10으로 나누어줍니다.
0은 어떤 수의 앞에 온다고 해서 이를 세주지 않으므로, i만큼 빼고 계산해야 합니다.
curr를 기준으로 왼쪽 숫자들은 위에서 구한대로 (N+1) * i개만큼 등장하며, curr를 기준으로 오른쪽 숫자들은 N * i개 등장합니다.
그리고 가장 중요한 curr는 add라는 수를 추가하여 이전 자릿수에서 얼마나 더 세주어야 하는지를 기록하도록 하였습니다.
N*i + 1에다가 add만큼 추가된 값을 cnt[curr]에 더해주면 됩니다.
위의 풀이 코드대로 풀이를 작성하여 제출해보면, 위의 기록으로 모든 테스트케이스를 통과할 수 있습니다.
+ Class 6 획득
결과적으로 Class 6의 문제들을 풀어서 Class 6을 획득하게 되었습니다.
기존 2203이라는 레이팅은 사실 너무 다이아 끝에 걸쳐있어서 아쉬운 점이 있었는데, 이번에 Class 6을 통과하면서 점수를 더 올려보고 싶다는 생각이 들기도 합니다.
시간이 난다면 Class 7 문제들에도 도전해보도록 하겠습니다.
'알고리즘 > 백준(BOJ) 문제풀이' 카테고리의 다른 글
| [백준/BOJ] 11051번 : 이항 계수 2, 9375번 : 패션왕 신해빈, 2004번 : 조합 0의 개수 (조합, 경우의 수) (0) | 2022.02.25 |
|---|---|
| [백준/BOJ] 2981번 : 검문, 3036번 : 링 (정수론, 조합론) (0) | 2022.02.25 |
| [백준/BOJ] 17371번 : 이사 (그리디 알고리즘, 기하학) (0) | 2022.02.24 |
| [백준/BOJ] 16565번 : N포커 (DP, 조합론, 포함과 배제의 원리) (0) | 2022.02.23 |
| [백준/BOJ] 5052번 : 전화번호 목록 (트라이, Trie) (0) | 2022.02.23 |