이 포스트에서는 LCA, 최소 공통 조상 알고리즘에 대한 구현과 예시 문제 풀이를 다루고 있습니다.
예시 문제로는, 프로그래밍 문제 사이트 백준 Online Judge의 11438번 : 'LCA 2' 문제에 대한 풀이 코드와 해설을 다루고 있습니다.
문제의 난이도는 Solved.ac 기준 Platinum V에 해당합니다.
11438번 : LCA 2
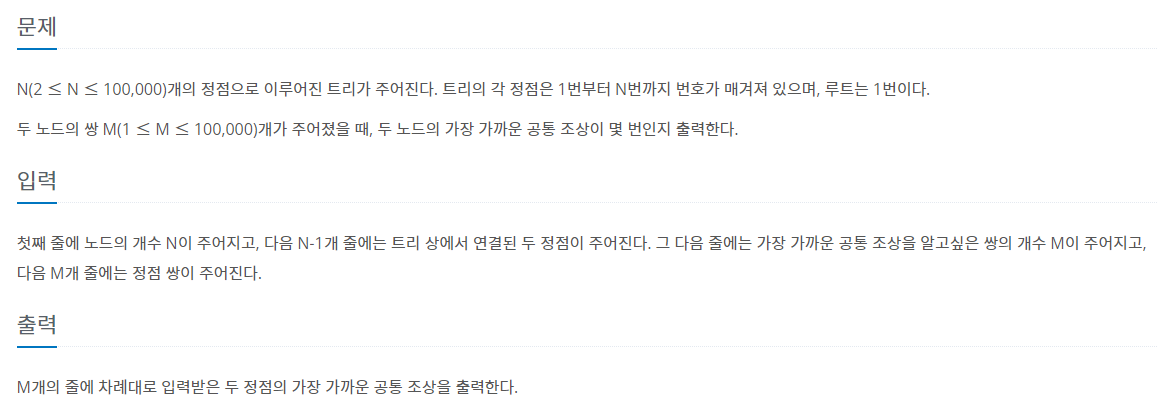
문제 자체가 LCA 알고리즘을 설명하기에 최적화 되어있는 문제이기에, 그냥 문제를 풀이하면서 설명해보도록 하겠습니다.
첫째 줄에 노드의 개수 N이 주어지고, N-1개의 트리 사이에 연결된 간선에 대한 정보가 주어져 트리가 입력됩니다.
이후 M개의 두 노드 쌍에 대해, 각 노드 쌍이 가지는 최소 공통 조상을 구해 출력해주는 문제입니다.
이 문제는 문제의 이름 그대로 LCA 알고리즘, 최소 공통 조상을 찾는 알고리즘을 구현하는 문제입니다.
따라서 문제 조건에 맞게 CA 알고리즘을 구현하고, 이에 대한 설명을 진행하도록 하겠습니다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
|
#include <cstdio>
#include <vector>
#define MAX 100001
using namespace std;
int Parent[MAX][20], Depth[MAX], H = 0;
vector<int> Line[MAX];
void findParent(int Par, int Node, int Dep) {
if(!Line[Node].size()) return;
Parent[Node][0] = Par;
Depth[Node] = Dep;
for(int i=0; i<Line[Node].size(); i++)
if(Line[Node][i] != Par) findParent(Node, Line[Node][i], Dep+1);
}
int findLCA(int A, int B) {
if(Depth[A] != Depth[B]) {
if(Depth[A] < Depth[B]) swap(A, B);
int Diff = Depth[A] - Depth[B];
for(int i=0; Diff>0; i++) {
if(Diff%2) A = Parent[A][i];
Diff >>= 1;
}
}
if(A != B) {
for(int i=H; i>=0; i--)
if(Parent[A][i] != 0 && Parent[A][i] != Parent[B][i]) {
A = Parent[A][i];
B = Parent[B][i];
}
A = Parent[A][0];
}
return A;
}
int main() {
int N, M, A, B;
scanf("%d", &N);
for(int i=0; i<N-1; i++) {
scanf("%d %d", &A, &B);
Line[A].push_back(B);
Line[B].push_back(A);
}
findParent(0, 1, 0);
int temp = N;
while(temp > 1) {
temp /= 2;
H++;
}
for(int i=1; i<=H; i++)
for(int j=2; j<=N; j++)
if(Parent[j][i-1]) Parent[j][i] = Parent[Parent[j][i-1]][i-1];
scanf("%d", &M);
for(int i=0; i<M; i++) {
scanf("%d %d", &A, &B);
printf("%d\n", findLCA(A, B));
}
}
|
cs |
- 그래프 입력
먼저 트리 사이의 간선에 대한 정보를 Line으로 입력받습니다.
이 때 N×N 배열을 선언하면 메모리가 초과되므로, 사용되는 칸만큼만 메모리를 사용할 수 있도록 벡터를 이용해줍니다.
모든 간선에 대한 정보를 입력했으면 이제 노드의 부모를 저장하기 위해 DFS 알고리즘을 사용해줍니다.
- findParent 함수
DFS의 방식으로 Parent[Node][0]에 Node의 부모 노드를 저장해주고, Depth[Node]에 Node의 깊이를 저장해줍니다.
자식 노드는 다음 재귀 호출에서 부모 노드가 되고, 자식 노드에 연결된 다른 노드가 새로운 자식 노드가 됩니다.
Depth는 findLCS 함수에서 두 노드의 높이를 맞춰주는 데에 사용합니다.
- Parent 배열 갱신
이 때 Parent를 저장하는 방식이 중요한데, 해당 노드로부터 1, 2, 4, 8, ... 위에 있는 노드 즉 2의 제곱이 되는 상위 단계의 노드만 저장합니다.
그 이유는 최악의 경우 트리가 1자로 연결이 되었을 때, 매번 노드를 하나씩 거슬러 올라가면 시간 초과가 발생할 수 있기 때문입니다.
반면 2의 제곱씩 상위 노드로 올라가는 방법을 이용하면, 13개 노드를 올라가야 한다고 할 때, 13을 이진수 1101로 바꾸고 처음에는 1*1개의 노드를 올라가고, 그 다음 2*0개의 노드를 올라가고(= 올라가지 않고), 그 다음 4*1개의 노드를, 그 다음 8*1개의 노드를 올라감으로써 log(H) 시간에 올라갈 수 있습니다.
이는 findLCA 함수에서 다시 사용할 것이므로, 우선은 Parent[Node][i]에 Node로부터 2^i 상위에 있는 부모 노드를 저장한다는 것만 확인하면 됩니다.
예를 들어 2^5 = 2^4 * 2^4 = 2^(5-1) * 2^(5-1)이므로, 이 원리를 이용하여 Parent[j][i] = Parent[Parent[j][i-1]][i-1]로 저장할 수 있습니다.
이 경우 몇 번 노드가 상위에 있고 하위에 있는지 모르므로, 모든 H 이하의 i에 대해, 모든 노드 j를 검사해줄 수밖에 없습니다.
- findLCA 함수
우선 Depth로 깊이차를 구하고, 더 깊은 노드를 A라고 둡니다.
그리고 위에서 말했듯 Depth를 이진수로 바꾸어, log(H) 시간 안에 높이를 맞춰주도록 Parent를 이용하여 올라가줍니다.
높이를 맞췄는데 우연히 같은 노드에서 멈춘 경우에는 그 노드가 LCA이므로 A를 리턴해주면 됩니다.
만약 아닌 경우에는 이제부터 똑같이 하나씩 올라가면서 두 부모가 동일할 때까지 반복해주면 됩니다.
위의 코드는 LCA가 존재하지 않는 경우도 무한루프에 걸리지 않고 빠져나오도록 설계되어 있습니다. (Parent가 0이면 LCA가 없는 것)
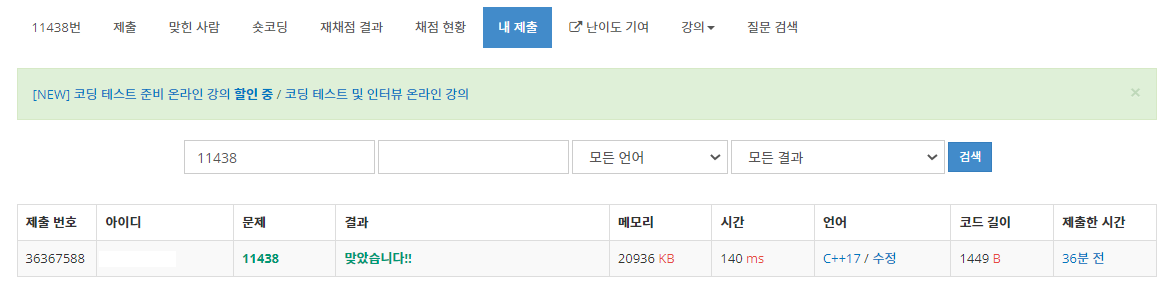
제출해보면 정답 처리를 받을 수 있습니다.
11437번 : LCA
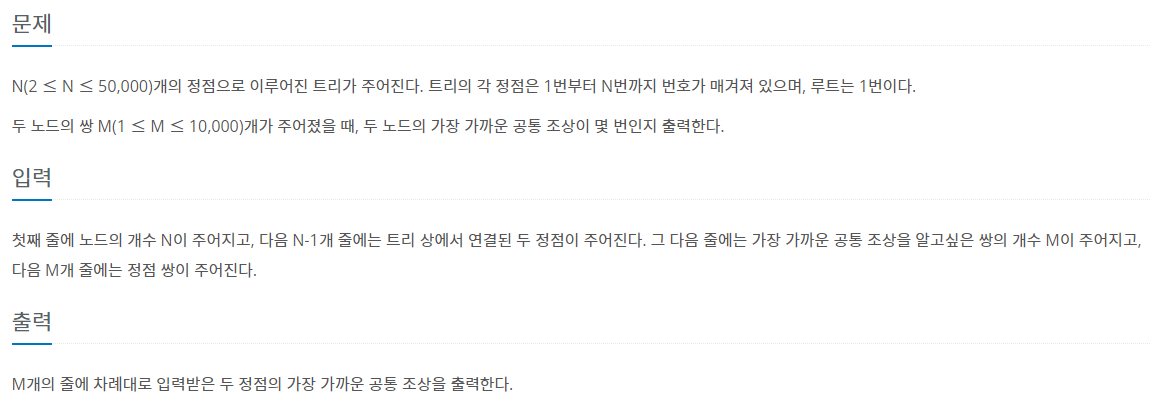
이 문제는 범위가 훨씬 작고, 시간 제한이 3초로 넉넉하게 주어집니다.
이 경우에는 위의 log(H)의 부모 노드 탐색 방법을 사용하지 않아도 해결이 가능합니다.
다만 더 일반화되어있는 알고리즘을 설명하기 위해 LCA 2의 풀이를 먼저 올렸습니다.
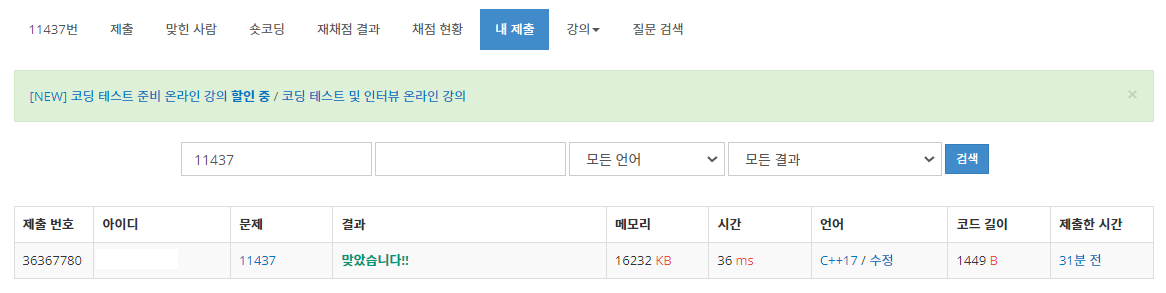
LCA 2의 풀이를 제출하면 역시 이 문제도 해결이 되는 것을 확인할 수 있습니다.
'알고리즘 > 알고리즘 공부 내용 정리' 카테고리의 다른 글
| 우선순위 큐를 활용한 다익스트라 알고리즘 O(E log V) (0) | 2022.03.28 |
|---|---|
| [웹 사이트 만들기] 웹 호스팅하기, 도메인(내 주소) 생성, 페이지 만들기 (0) | 2022.03.14 |
| [C++ 알고리즘] 각종 알고리즘의 외워두면 유용한 정석 코드 모음 (0) | 2021.12.25 |
| C언어 모든 정렬 알고리즘 가장 간단한 코드 정리 (순차, 버블, 삽입, 선택, 병합, 퀵 정렬) (0) | 2021.11.17 |
| [C언어 재귀함수] 10진수를 2진수로 변환하는 2줄짜리 함수 코드 (2) | 2021.08.08 |