PEET 일반물리 모든 회차 기출문제 중 개인적으로 풀었던 문제들 중 틀리거나 어려웠던 문제만 뽑아서 정리합니다.
2011학년도 5번


PV = nRT 식 하나로는 미지수가 2개이기 때문에 풀리지 않습니다.
따라서 에너지 보존 식까지 같이 써줘야 연립해서 P'을 구할 수 있습니다.
2011학년도 6번


보기 ㄷ을 풀기 위해 엔트로피 적분 식을 알고 있어야 △Q = T△S임을 알아낼 수 있습니다.
2011학년도 8번


파동의 속도가 빠를수록 굴절이 덜 일어납니다.
또한 보기 ㄴ에서 물체와 볼록렌즈 사이의 거리가 가까워지면 도립 실상에서 정립 허상으로 바뀜에 주의해야 합니다.
2011학년도 9번


보기에서 단일 슬릿의 끝과 끝 사이를 언급하는지, 중간과 끝 사이를 언급하는지에 주의하여 문제를 풀이해야 합니다.
2011학년도 13번


전체 회로의 V 값은 일정함을 이용하여 V_R 값을 마지막에 구해주어야 합니다.
2011학년도 15번


전자는 에너지 장벽을 투과하고 난 뒤에는 다시 파동성을 가진다는 사실을 알아야합니다.
무한 퍼텐셜 장벽과 유한 퍼텐셜 장벽 사이의 차이에 유의해야합니다.
2012학년도 2번


보기 ㄱ에 해설을 잘못 적었는데 물체에 마찰력이 작용했음에도 물체가 정지해있다면 마찰력은 μ_s mg 이하입니다.
2012학년도 3번


E = △mc^2 공식에서의 △m은 원자량과 관계없이 반응에서 결손되는 질량을 말합니다.
(공식의 기호가 어떤 의미를 가지는지 잘 생각해볼 것)
2012학년도 5번


자유 팽창에서 온도는 변하지 않으며, P, V만 변화함에 주의해야합니다.
또한 엔트로피는 상태수에 비례하므로 온도와 관계없습니다. (분자가 빠르게 이동한다고 해서 상태 수가 증가하는 것이 아님)
다만 △S 값은 온도에 의존됨에는 유의해야합니다.
2012학년도 7번


개관 내에서 압력 그래프 또한 정상파와 같은 개형으로 작용함을 알아야합니다.
2012학년도 13번


RLC 회로에서 전체 임피던스가 아닌 두 점 사이의 임피던스를 계산할 때는 그 사이 점에 있는 임피던스 요소(R, L, C)들의 임피던스만을 계산하면 됩니다.
2013학년도 4번


간단한 베르누이 방정식을 세울 때에도 문제 조건을 명확하게 읽지 않으면 틀리게 되니 정확히 식을 세우는 것이 중요합니다.
2013학년도 5번


2차원 운동 문제를 풀 때는 가장 간단하게 해결할 수 있는 방식으로 식을 세워야합니다.
공식이 여러 개가 있지만 그 중 최선의 공식을 선택하여 사용하는 연습이 필요합니다.
2013학년도 17번


T_H와 T_L을 구할 필요 없이 두 상태 사이의 절대온도 비만 알아도 열량비, 열효율 등을 구할 수 있으니 비율을 구하는 것에 초점을 두어야합니다.
2014학년도 7번


회로에서 전지의 +극에서 -극까지의 경로에서 전류가 축전기를 반드시 지나야하는지를 통해 전류가 흐르는 상태를 구분할 수 있습니다.
(나)의 상황에서 스위치가 닫히면 전류는 세 개의 저항을 직렬로 통과하여 -극까지 흐를 수 있으므로 a에 전류가 흐르고 있는 상태입니다.
2014학년도 9번


RC 회로에서 I 그래프에 대해서도 알아두어야합니다. (Q, V_c 그래프와 반대로 나타남)
2014학년도 10번


상평형과 열량 문제가 나올 때는 공식 자체는 매우 쉬우나 단위 환산이나 크기 비교에서 헷갈리거나 실수하지 않도록 주의해야합니다.
2014학년도 12번


보기 ㄱ에서 등적 과정에 대응되는 그래프가 찾아지지 않을 때는 다른 명확한 근거가 있는 구간 먼저 대응시키면 됩니다.
2014학년도 17번


빛의 세기는 광자의 수에 비례하므로, 이 또한 고려해주어야 합니다.
2015학년도 4번


베르누이 방정식 문제에서는 두 지점 사이의 압력차를 구할 때 P항만 넘기고 나머지 기호들을 모두 넘겨 계산해주어야합니다.
2015학년도 9번


파동의 속도가 빠를수록 굴절이 덜 일어나고, 파동의 속도가 느릴수록 굴절이 더 일어납니다.
(속도가 빠르면 주변 환경의 저항을 덜 받는다는 느낌으로 외우면 쉬움)
또한 속도가 느린 빛이 전반사 임계각이 더 작으므로, 더 넓은 각도에서 전반사가 일어납니다.
보기 ㄷ처럼 어떤 값을 주고 비교하는 문제는, 보기에 제시된 기호 말고 비교가 쉬운 다른 문자로 비교하는 것이 쉽습니다.
2015학년도 12번


문제에서 전위를 말하는 것인지, 전기장을 말하는 것인지 구분을 잘 해서 문제를 풀어야합니다.
이 문제에서는 전위에 대해 물었으므로, 분모의 거리 값의 부호를 조심해서 풀어주어야 합니다.
2015학년도 14번


이 문제에서 도선 A에 작용하는 자기력을 구하기 위해서는 여러 지점에서 작용하는 자기력들을 두 세 개 정도 그려본 뒤 그 합력 방향을 구해야합니다.
2015학년도 16번


축전기 옆에 저항이 직렬로 연결되어 있더라도 그 밖의 병렬 구조를 크게 잡아서 축전기에 걸리는 전압을 구해주어야 합니다.
보기 ㄴ에서 P에 흐르는 전류의 "최댓값"을 물었으므로, 축전기가 충전 중일 때와 방전 중일 때 두 상황에서의 최댓값을 모두 구해 비교해주어야 합니다.
보기 ㄷ에서 축전기의 전하량은 전압에 비례하므로, 축전기의 전하량이 절반뿐이라면 축전기에 의해 회로에 걸리는 전압 또한 절반입니다.
2015학년도 19번


광전자 일함수 공식을 사용할 때 기호가 많기 때문에 물질파의 제곱에 반비례한다는 특성을 이용해야 두 식을 연립할 수 있습니다.
또한 물질파 파장이 같으면 운동에너지 또한 같음을 적용해야 문자를 줄여 식을 풀 수 있습니다.
2016학년도 2번


이런 단순 계산인 것 같은 문제가 나올 때는 더 빨리 풀 수 있는 방법이 있다고 의심하지 말고 식을 여러 개 써서 연립을 바로 하던가, 아니면 문제를 빨리 포기하고 넘기는 것이 중요할 것 같습니다.
또한 이러한 여러 공식들이 얽혀 있는 연립 계산 문제를 풀 때는 비례 관계를 찾아서 기호를 빠르게 줄여주는 것이 중요합니다.
2016학년도 7번


도플러 식에서는 항상 분자, 분모 구분과 +, - 부호 구분, 그리고 계산 실수를 조심해야 합니다.
2016학년도 9번


고유 진동수에 관한 문제입니다.
고유 진동수에서는 항상 전류가 최대이고, 유도 리액턴스와 용량 리액턴스가 같다는 성질을 이용해주어야 합니다.
또한 xf_0일 때와 1/x f_0일 때 전류 값이 같고, 유도 리액턴스와 용량 리액턴스 값이 서로 반대임을 유의하여 방정식을 세워주어야 합니다.
2016학년도 10번


이 문제에서는 용수철이 혼자 이동하기 때문에 상대 속도와 운동량 보존 식을 적절히 잘 써야 합니다.
우선 나무 도막 분리 전에는 운동량 보존에 의해 A는 왼쪽으로 2v, B, C는 오른쪽으로 v로 이동합니다.
분리 후에는 A, B가 하나로 이동하고 C만 따로 분리되므로 C가 v로 이동할 때 A, B는 -v/2로 이동합니다.
2016학년도 13번


유체역학 문제는 Av 일정, 베르누이 방정식만 잘 써주면 됩니다.
2016학년도 14번


이 문제의 핵심은 보기 ㄴ인데요, 전위의 정의 자체가 무한 원점에서 전하를 끌고 오는데 드는 힘이므로, 도체를 통과할 때는 전위가 변하지 않음을 유의해야합니다.
즉, 위 문제 상황에서 점전하로부터 2R, 3/2R, R 모두에서 전위는 같습니다.
2016학년도 17번


단열 과정에서 PV^γ 일정, TV^(γ-1) 일정 두 식을 가지고 VT 관계식도 유도할 줄 알아야 보기 ㄱ을 빠르게 풀 수 있습니다.
또한 이 문제에서는 등적 몰비열 C_v = 5/2 R이므로 △U를 구하는 과정에서 계수를 다르게하여 풀어주어야 합니다.
2016학년도 19번


이 문제는 첫 번째로는 전기장 방향을 빠르게 찾는 것이 중요하고,
그 다음 물질파 식으로부터 운동에너지 변화량 식을 빠르게 유도하여 각 변수의 비율에 따른 운동에너지를 정확히 비교해주는 것이 중요합니다.
변수가 많고 비교 대상이 많으므로 헷갈리기 쉽습니다.
2016학년도 20번


알파 붕괴, 베타 붕괴, 감마 붕괴에 대해서도 헷갈리지 않도록 암기하고 있는 것이 중요합니다.
특히나 감마 입자와 중성미자의 비교를 헷갈리지 않아야합니다.
2017학년도 8번


이 문제는 두 물체가 동일한 가속도를 아래로 받음을 아는 것이 가장 중요합니다.
그렇지 않고 두 물체 각각에 중력가속도를 적용하여 문제를 접근하면 식이 매우 복잡해지기 때문입니다.
또한 탄성 충돌의 경우 상대 속도 차이가 그대로라는 특성 또한 알고 있어야 문제를 더욱 간단하게 해결할 수 있습니다.
2017학년도 16번


수소 원자 에너지 준위 문제에서 특히나 파장 크기와 에너지, 결합 길이와 에너지 등 목적어가 무엇인지 유의해서 보기를 읽어야 합니다. (생각보다 많이 실수함)
2017학년도 20번


카르노 기관의 열효율을 구할 때 온도비는 등온 과정에서 PV 값의 비율과도 같다는 성질을 이용해야 문제를 간단하게 풀 수 있습니다.
보기 ㄷ에서는 두 상태의 온도비를 부피비를 이용하여 간접적으로 계산하였고, 이러한 아이디어를 많이 활용해야 시간을 단축할 수 있습니다.
각각의 단열 과정에서의 두 상태의 V, T 값을 빠르게 계산할 줄 알아야 제 시간에 풀 수 있는 문제입니다.
2018학년도 7번


충전 중인 축전기는 끊긴 전선이나 마찬가지이고, 코일은 저항 0인 전선과 마찬가지임을 알아야 해결할 수 있는 문제입니다.
또한 두 회로에서 어떤 쪽의 전류가 4I_0이고 어떤 쪽의 전류가 3I_0인지 모르기 때문에 빠르게 4:3으로 두고 계산한 뒤 정답이 가정에 모순이 되면 다시 계산해주면 됩니다.
2018학년도 9번


(가)의 B와 (나)의 A는 고려해야할 힘과 변수가 매우 많고, 2개의 식만 있어도 3개의 문자 사이의 관계식을 이끌어낼 수 있기 때문에 (가)의 A, (나)의 B 두 개의 물체에 대한 힘 평형 식만 고려해주면 됩니다.
2018학년도 12번


보기 ㄷ이 헷갈릴 수 있는데, 우선 점 P는 t=0일 때 변위가 -A인 지점이고, T/3이 지난 이후에는 1/3 파장만큼이 지나간 뒤이고, t = T/4일 때 정확히 변위가 음수에서 0이 되므로, t = T/3일 때 변위는 0보다 커야합니다.
2018학년도 14번


이 문제는 거울로 반사되는 상황을 슬릿 간 간격이 2d인 이중 슬릿에서 실험하는 상황으로 변형시켜 생각하는 아이디어를 사용하지 않으면 매우 어려워지므로, 상황을 단순하게 변화시키는 아이디어가 중요합니다.
여기에 거울에서 반사가 한 번 일어날 때 고정단 반사가 발생하므로 위상이 180도 변화함 또한 적용시켜야 합니다.
보기 ㄷ에서 거울의 위치를 +y 방향으로 λ만큼 이동시키면 경로차가 2xλ/L만큼 증가하고, 이 때 문제에서 제시된 수치 근사를 사용해야 정답을 얻을 수 있습니다.
2018학년도 20번

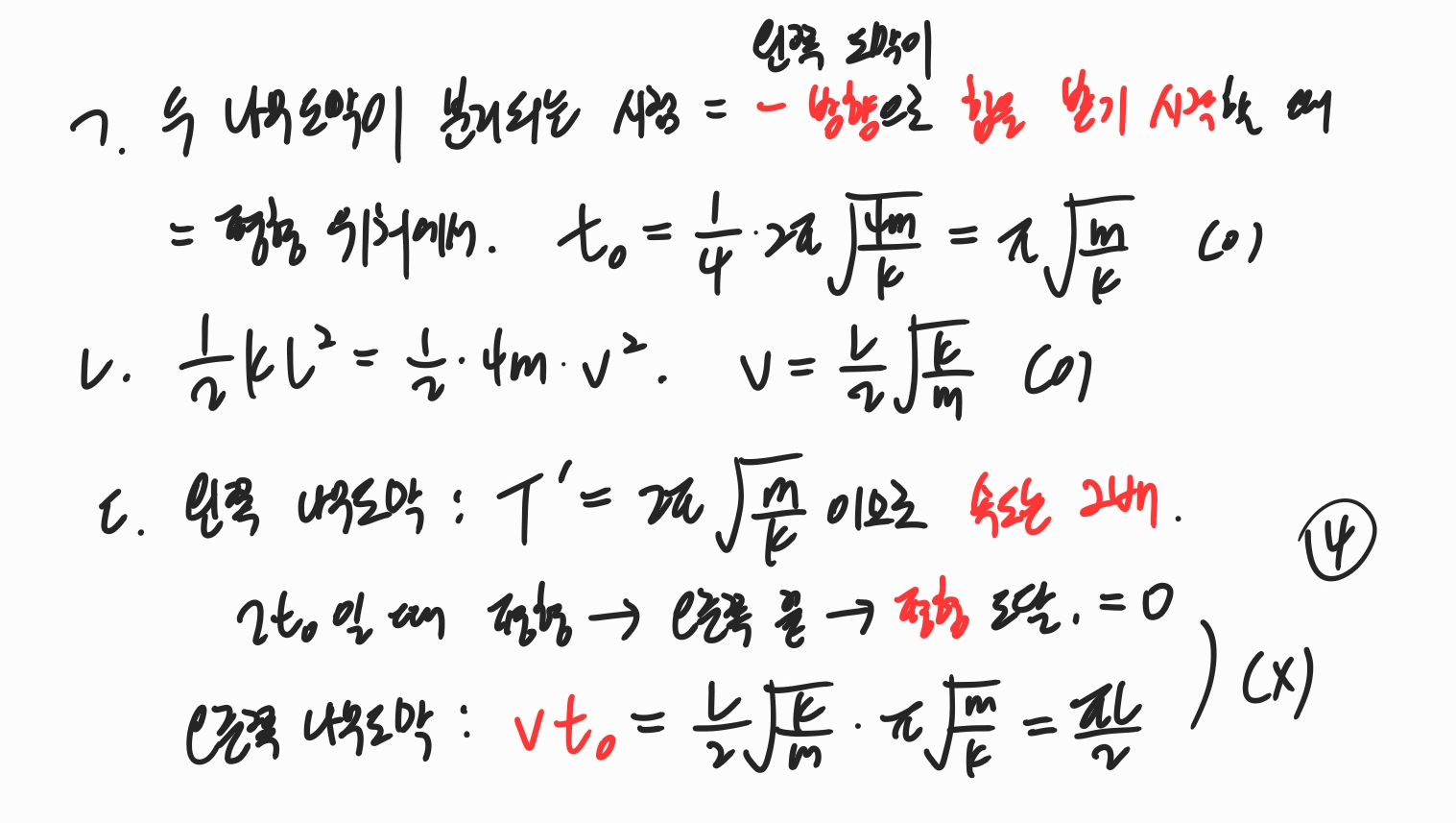
용수철에 두 나무 도막이 동시에 이동할 경우, 두 나무 도막이 분리되는 시점은 왼쪽 도막이 (-) 방향으로 힘을 받기 시작하는 시점, 즉 용수철이 최대로 늘어났을 때입니다.
보기 ㄷ에서는 나무 도막이 분리된 시점부터 T' = 2T임과, 2t_0일 때 왼쪽 나무 도막이 평형에 도달할 시점임을 알아야 두 나무 도막 사이의 거리를 vt_0라는 간단한 식으로 계산할 수 있습니다.
2019학년도 11번


도플러 효과 문제에서는 언제나 변수가 분자, 분모에 들어갈 상황을 정확히 구분하고 각 상황에서 멀어지는지 가까워지는지에 따라 부호를 정확히 구분하여 실수가 없도록 해야 합니다.
보기 ㄷ에서는 두 상황 모두 분자 분모에 부호가 적용되므로 크기 비교 시 실수가 없도록 주의해야 합니다.
2019학년도 14번
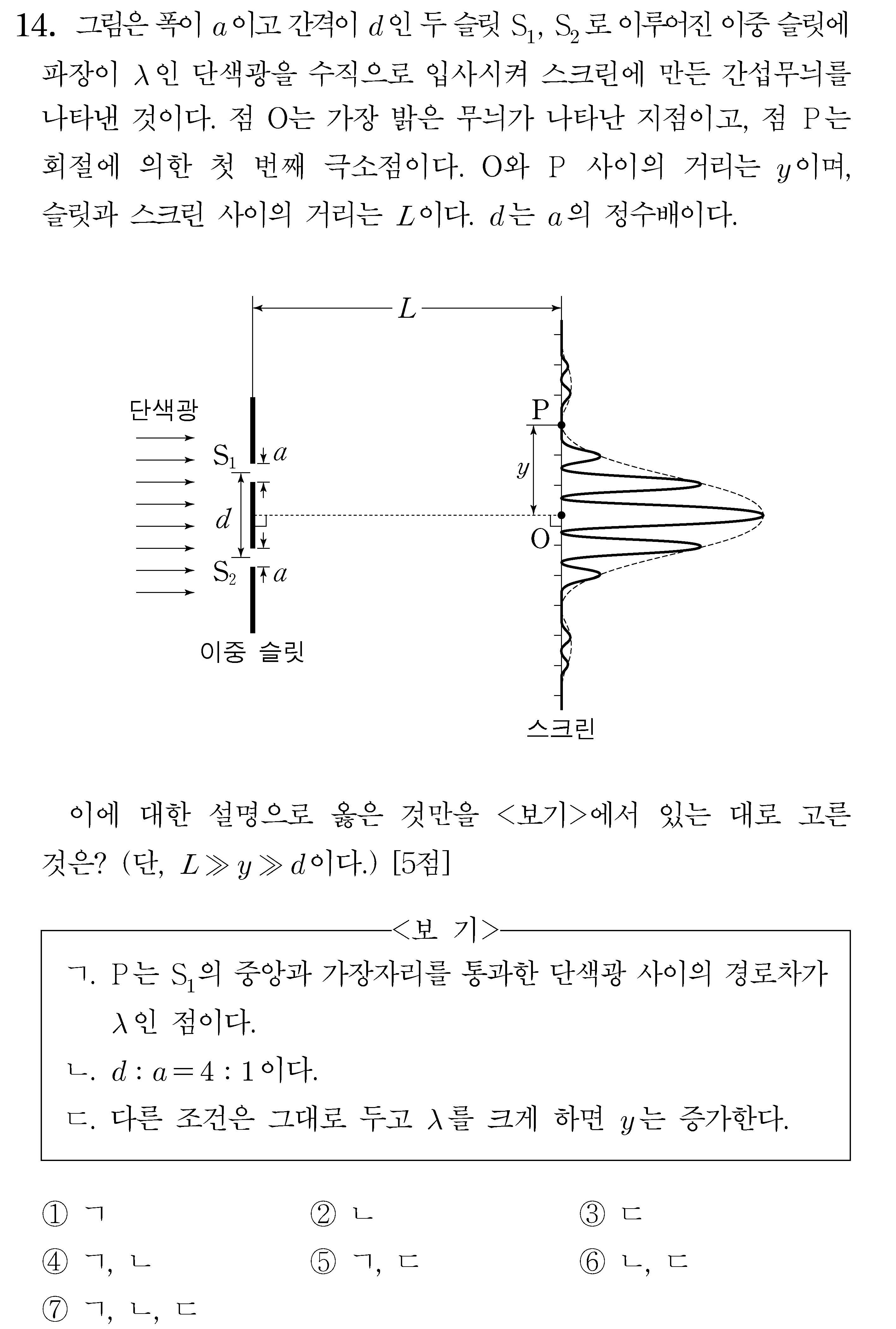

단일 슬릿이나 이중 슬릿 간섭 문제에서는 슬릿의 끝과 끝 사이의 경로차를 물었는지, 끝과 중간 사이의 경로차를 물었는지에 유의하여 문제를 풀이해야 합니다.
이중 슬릿 간섭 실험에서 두 파장이 상쇄되는 지점은 dλ/L이고, 중심으로부터 (중심을 제외한) 첫 번째 극대점은 aλ/L입니다.
이 둘의 정수비를 통해 d : a 값을 구할 수 있습니다.
2019학년도 18번


퍼텐셜 우물에서 입자의 에너지는 바닥 상태의 에너지 + 입자의 운동 에너지입니다.
유한 퍼텐셜 우물에서는 항상 터널링 효과가 발생합니다.
2019학년도 19번


부피가 감소하면 항상 음의 일, 즉 일을 받는 상황입니다.
보기 ㄱ에서 적분을 수행할 때 P에 대한 변수를 r에 대한 변수로 바꿀 수 있고, dV 또한 4πr^2dr로 변환 가능하므로 r에 대한 적분을 수행하여 일의 양을 구할 수 있습니다.
보기 ㄷ에서 방출한 열량을 구할 때는 보기 ㄱ에서 구한 일의 양에 새로 계산한 △U 값을 더해주면 됩니다.
2019학년도 20번


운동량 보존은 어느 상황에서나 사용이 가능하고, 에너지 보존에 비해 식이 단순하므로 위의 문제와 같은 상황에서 사용합니다.
보기 ㄴ에서 가장 중요한 포인트는 질량 m의 나무 도막은 질량 2m의 45도 "경사면을 따라서" 내려가므로 x축 방향 상대속도와 y축 방향 상대속도가 동일하다는 것입니다.
이를 이용하여 v_y = 3v임을 알아낼 수 있고, 이를 바탕으로 v를 계산해줄 수 있습니다.
2020학년도 7번


콤프턴 효과 문제는 식이 3가지나 되고, 변수가 많기 때문에 변수를 빨리 줄이는 연습을 해야 합니다.
또한 이 문제에서 마지막 부분에 산란 전 광자의 에너지 E = mc^2 = hc/λ_0을 줬는데, 문제를 급하게 읽으면 이러한 조건을 빠뜨려 식이 절대로 안 풀리니 문제를 주의해서 읽어야 합니다.
2020학년도 8번


축전기 양단에 걸리는 전압은 V = ΣIR로 계산할 수 있고, 이 때 전류는 굳이 계산하지 않아도 그 비율만 가지고 계산하면 됩니다.
2020학년도 10번


간단한 문제이지만 물체가 최고점에서 정지한다고 하여 힘을 받지 않는다는 실수를 하면 안됩니다.
문제의 C 상황에서 돌고래는 아래로 mg의 힘을 항상 받고 있습니다.
2020학년도 15번


위 실험에서 전지와 전원 장치에서는 가변 저항에 서로 같은 극이 같은 방향으로 연결되어야 합니다.
또한 이러한 실험을 응용하여 휘트스톤 브릿지와 관련된 실험을 구성할 수도 있으니 참고하시면 좋습니다.
2020학년도 17번


dB/dt를 계산할 때 식으로 생각하지 않고 보기 ㄷ에서의 풀이처럼 그래프를 그려서 생각하면 헷갈리지 않고 간편합니다.
PEET 일반물리 시험은 일반적으로 값을 식을 통해 계산해내는 것보다는 두 변수 사이의 관계나 크기 비교를 위주로 물어보기 때문에 식보다는 그래프로 비교하는 것이 편할 때도 있습니다.
2020학년도 18번


점 p는 단일 슬릿 끝과 끝 사이 경로차가 2ap/L이고 이것이 λ인 지점입니다.
점 q는 이중 슬릿의 두 슬릿 사이 경로차가 4aq/L이고 이것이 5λ/2인 지점입니다.
점 r은 단일 슬릿 끝과 끝 사이 경로차가 ar/L이고 이것이 λ인 지점입니다. (원래는 이중 슬릿 간섭이 극대로 나타나는 지점이지만, 단일 슬릿 내에서 끝과 끝 사이 경로차가 λ이어서 세기가 0으로 나타나는 지점)
2020학년도 19번


Q나 EdA 적분 식에서 각 변수를 다른 변수로 치환해주는 것이 중요한 문제입니다.
2020학년도 20번


빗면에서 마찰력이 작용할 때 관성 모멘트가 있는 물체의 구름 운동에 대한 식 3개를 연립하여 풀이해주면 간단하게 풀 수 있지만, 모르면 어려울 수 있는 문제입니다.
그리고 s-t 그래프에서 그래프 개형이 1/2 at^2임을 인지하고 a 값을 구해주어야 합니다.
보기 ㄴ에서 각운동량의 크기는 Iω로 구해도 되고, rmv로 구해도 됩니다.
2021학년도 9번


계에서 모든 힘을 정확히 표현해야 F에 대응되는 힘인 T를 확인할 수 있습니다.
다른 물체에 대한 운동 방정식은 어렵지 않으나 F=T임을 알아야 풀 수 있는 문제입니다.
2021학년도 11번


편광 파트는 중요도가 낮아 지속적으로 봐두지 않으면 헷갈릴 수 있습니다.
어떤 광원에서 나오는 빛은 항상 무작위적으로 비편광되어 있으며, 편광축을 지날 때 I = I_0 cos^2θ의 세기를 가지며 편광축에 평행하게 편광됩니다.
2021학년도 15번


구름 운동을 할 때 물체가 미끄러지며 마찰력이 일을 하는 것이 아니므로 역시 역학적 에너지는 보존됩니다.
(가)에서는 위치에너지가 모두 병진 운동 에너지로 사용되지만, (나)에서는 위치에너지가 병진 운동 에너지와 회전 운동 에너지로 분산되기 때문에 속도가 더 느립니다.
따라서 물체가 정지하는데까지 걸리는 시간이 다릅니다.
2021학년도 16번


프리즘에서 빛의 굴절 문제에서는, 항상 도형의 성질을 이용해 각을 먼저 구해주는 것이 중요합니다.
또한 보기 ㄴ에서와 같이 굴절률 또는 각의 크기를 비교하는 상황일 때는 각각의 각이 증가하는지 또는 감소하는지만 빠르게 체크해주고 넘어가는 것이 중요합니다.
2021학년도 19번


보기 ㄱ에서 상황 설정을 할 때 변수를 V가 아닌 2V로 두면 계산할 때 조금 더 편합니다.
A에만 열이 가해졌으므로 B를 단열 조건으로 풀이한 뒤, V_A = V_tot - V_B와 같은 방식으로 A의 변수를 구해주어야 합니다.
단열 과정에서 엔트로피 변화는 없습니다.
2021학년도 20번


이 문제에서는 운동 에너지에 대한 변수를 E_k로 두고 미분해서 극대값을 구하는 아이디어를 사용해야 합니다.
이처럼 PEET 일반물리에서는 간단해보이지만 치환 적분이나, 미분을 통한 극대/극소값을 찾는 등의 아이디어를 활용할 줄 알아야합니다.
질문 사항 있으시면 댓글로 남겨주시면 도움을 줄 수 있는 범위 내에서 도와드리겠습니다.
'자연과학(PEET) > 요약 정리 자료' 카테고리의 다른 글
| [PEET 자료] 시험 대비 전체 범위 정리 요약본 - 기출 문제에 없는 개념 (+ 시험 시간 분배, 찍기 특강) (9) | 2021.08.17 |
|---|---|
| [PEET 유기화학] 유기화학 전 범위 반응식 한 장 정리 요약 (파일 첨부) (2) | 2021.07.07 |
| [PEET 일반화학] 일반화학 전 범위 공식 한 장 정리 요약 (파일 첨부) (2) | 2021.07.07 |
| [PEET 일반물리] 일반물리 전 범위 공식 한 장 정리 요약 (파일 첨부) (0) | 2021.07.07 |
| [PEET 생명과학] 일반생명과학 전 범위 기출 문제 등장 개념들 정리 (2) | 2021.07.01 |