11월 말 백준에서 풀이한 문제들 중, 플래티넘 이상 난이도 문제들에서 다른 사람들이 잘 다루지 않는 내용들을 선별하여 정리해보려고 한다.
이번 기간에 다룬 알고리즘은 MCMF(최소 비용 최대 유량)이다.
낮은 난이도나 다른 사람들이 많이 푼 문제들은 이미 다 풀어서 플래티넘 난이도 중에서도 어려운 것만 남았고, 그에 대한 풀이를 다룬 사람들이 별로 없어서 간략하게나마 적어본다.
어디까지나 스스로 공부, 잊어버렸을 때 나중에 다시 참고하기 위한 목적이지만 혹시나 검색 유입으로 보는 사람이 있다면 도움이 될 수 있으면 좋겠다.
백준 BOJ 14424번 : 두부장수 장홍준 3
문제 난이도 : Diamond V
알고리즘 분류 : MCMF (최소 비용 최대 유량)
사실 이 문제는 이전에 백준 BOJ 11111번 : 두부장수 장홍준 2 문제에 대한 풀이를 다룬 적이 있다.
다만 이 문제에서는 N, M의 제한이 50에서 200으로 늘어났고, 11111번 문제의 풀이 코드를 제출하면 일반적으로는 시간 초과에 걸리게 된다.
이 문제를 풀기 위해서는 기존 MCMF 알고리즘에 대해 최적화가 조금 더 이루어진 코드가 필요하다.
Dinic 알고리즘과 같이 유량을 갱신함과 동시에 새로운 DAG를 O(V+E) 시간에 갱신하는 최적화된 MCMF에 대한 구현을 찾을 수 있어 이를 참고하여 풀이하였다. (jhnah917님의 블로그에서 참고하였다. 처음부터 다시 작성했고 구조가 많이 다르긴 하지만 사실 본질은 거의 똑같이 구현되긴 했다.)
정형화시킨 코드는 팀노트(?)라고 부르기는 애매하지만 아무튼 오른쪽 카테고리의 "알고리즘 구현 코드 모음"의 MCMF 파트에 정리되어 있다.
#include <bits/stdc++.h>
#define int long long
using namespace std;
struct sm {
// referred to the jhnah917's implementation (purpose of study)
struct se { int num, cap, sco, ord; };
vector<vector<se>> adj;
void edge(int a, int b, int c, int d) {
adj[a].push_back({b, c, d, adj[b].size()});
adj[b].push_back({a, 0, -d, adj[a].size()-1});
}
int sour, sink;
vector<int> tco, idx;
vector<bool> chk;
int dfs(int x, int flo) {
chk[x] = true;
if(x == sink) return flo;
for(; idx[x] < adj[x].size(); idx[x]++) {
se &ad = adj[x][idx[x]];
if(chk[ad.num] || tco[x] + ad.sco != tco[ad.num] || ad.cap == 0) continue;
int ret = dfs(ad.num, min(flo, ad.cap));
if(ret == 0) continue;
ad.cap -= ret;
adj[ad.num][ad.ord].cap += ret;
return ret;
}
return 0;
}
pair<int, int> mcmf(int sour_, int sink_) {
sour = sour_, sink = sink_;
int minc = 0, maxf = 0;
tco.resize(adj.size(), INT_MAX);
tco[sour] = 0;
queue<int> q;
q.push(sour);
vector<bool> inq(adj.size());
inq[sour] = true;
while(!q.empty()) {
int x = q.front();
q.pop(); inq[x] = false;
for(int i=0; i<adj[x].size(); i++) {
int y = adj[x][i].num;
int cap = adj[x][i].cap;
int sco = adj[x][i].sco;
if(cap <= 0 || tco[x] + sco >= tco[y]) continue;
tco[y] = tco[x] + sco;
if(inq[y]) continue;
q.push(y);
inq[y] = true;
}
}
while(true) {
chk.clear(); chk.resize(adj.size());
idx.clear(); idx.resize(adj.size());
while(true) {
int cur = dfs(sour, INT_MAX);
if(cur == 0) break;
minc += tco[sink] * cur;
maxf += cur;
chk.clear(); chk.resize(adj.size());
}
int Min = INT_MAX;
for(int i=0; i<adj.size(); i++) {
if(!chk[i]) continue;
for(int j=0; j<adj[i].size(); j++) {
int x = adj[i][j].num;
int cap = adj[i][j].cap;
int sco = adj[i][j].sco;
if(cap > 0 && !chk[x]) Min = min(Min, tco[i] + sco - tco[x]);
}
}
if(Min == INT_MAX) break;
for(int i=0; i<adj.size(); i++)
if(!chk[i]) tco[i] += Min;
}
return {minc, maxf};
}
};
main() {
ios_base::sync_with_stdio(false);
cin.tie(NULL), cout.tie(NULL);
int N, M; cin >> N >> M;
vector<vector<char>> v(N+1, vector<char>(M+1));
for(int i=1; i<=N; i++)
for(int j=1; j<=M; j++) cin >> v[i][j];
sm f;
f.adj.resize(N*M + 3);
int sour = N*M + 1, sink = N*M + 2;
int cvt[6][6] = {{10, 8, 7, 5, 0, 1},
{8, 6, 4, 3, 0, 1},
{7, 4, 3, 2, 0, 1},
{5, 3, 2, 2, 0, 1},
{0, 0, 0, 0, 0, 0},
{1, 1, 1, 1, 0, 0}};
for(int i=1; i<=N; i++)
for(int j=1; j<=M; j++) {
if((i + j) % 2 == 0) {
f.edge(sour, (i-1)*M + j, 1, 0);
f.edge((i-1)*M + j, sink, 1, 0);
int di[4] = {1, -1, 0, 0};
int dj[4] = {0, 0, 1, -1};
for(int k=0; k<4; k++) {
int ni = i + di[k];
int nj = j + dj[k];
if(ni < 1 || nj < 1 || ni > N || nj > M) continue;
f.edge((i-1)*M + j, (ni-1)*M + nj, 1, -cvt[v[i][j]-'A'][v[ni][nj]-'A']);
}
}
else f.edge((i-1)*M + j, sink, 1, 0);
}
pair<int, int> mcmf = f.mcmf(sour, sink);
int minc = mcmf.first;
int maxf = mcmf.second;
cout << -minc << "\n";
}
백준 BOJ 5892번 : Landscaping
문제 난이도 : Platinum V
알고리즘 분류 : MCMF (최소 비용 최대 유량)
이 문제는 애초에 내가 질문 글을 올렸으니 그 이미지를 첨부한다.

이런 문제인데 아무튼 정석 풀이는 DP이고, 그래서 난이도가 Platinum V이다.
질문 글을 올리고 다음 날 답변이 달렸는데 이 문제를 유일하게 MCMF로 푸신 djs100201님이 풀이를 거의 떠먹여주시다시피 알려주셔서 구현해볼 수 있었다.
MCMF로 푸는 방법은 다음과 같다.
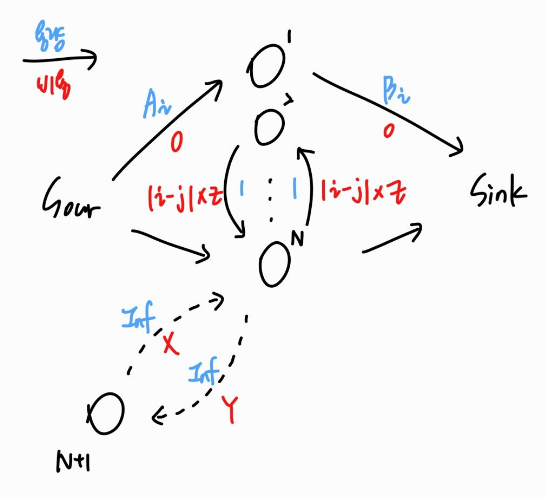
X와 Y를 처리할 노드를 하나 만들어서 마음껏 처리할 수 있도록 해준다.
그 다음 A_i값들의 합 asum과 B_i값들의 합 bsum을 구해 만약 asum이 더 크다면, (asum - bsum) x Y만큼 답에 더해준다.
반대의 경우에는 (bsum - asum) x X만큼 답에 더해준다.
대충 생각했을 때는 X, Y 값이 Z보다 매우 작을 경우 예외가 발생할 것 같기도 한데, 따로 연결한 노드 하나에서 그러한 예외가 모두 처리되기 때문에, 우선 최대한 싸게 이동을 시킨 뒤 마지막에 추가 또는 제거를 해도 답에 영향을 주지 않는다.
#include <bits/stdc++.h>
#define int long long
using namespace std;
struct se {
int num, ord, cap, sco;
se(int num, int ord, int cap, int sco) : num(num), ord(ord), cap(cap), sco(sco) {}
};
vector<vector<se>> adj;
int maxf, minc;
void edge(int a, int b, int c, int d) {
adj[a].emplace_back(b, adj[b].size(), c, d);
adj[b].emplace_back(a, adj[a].size()-1, 0, -d);
}
void mcmf(int sour, int sink) {
while(true) {
vector<int> pre(adj.size(), -1), idx(adj.size(), -1);
vector<int> tco(adj.size(), INT_MAX);
tco[sour] = 0;
queue<int> q;
q.push(sour);
vector<bool> inq(adj.size());
inq[sour] = true;
while(!q.empty()) {
int x = q.front();
q.pop();
inq[x] = false;
for(int i=0; i<adj[x].size(); i++) {
int y = adj[x][i].num;
int cap = adj[x][i].cap;
int sco = adj[x][i].sco;
if(cap <= 0 || tco[x] + sco >= tco[y]) continue;
tco[y] = tco[x] + sco;
pre[y] = x;
idx[y] = i;
if(inq[y]) continue;
q.push(y);
inq[y] = true;
}
}
if(pre[sink] == -1) break;
int sfl = INT_MAX;
for(int i=sink; i!=sour; i=pre[i]) {
int a = pre[i], b = idx[i];
sfl = min(sfl, adj[a][b].cap);
}
for(int i=sink; i!=sour; i=pre[i]) {
int a = pre[i], b = idx[i];
adj[a][b].cap -= sfl;
adj[i][adj[a][b].ord].cap += sfl;
minc += sfl * adj[a][b].sco;
}
maxf += sfl;
}
}
main() {
ios_base::sync_with_stdio(false);
cin.tie(NULL), cout.tie(NULL);
int N, X, Y, Z; cin >> N >> X >> Y >> Z;
vector<int> v(N+1), u(N+1);
int vsum = 0, usum = 0;
for(int i=1; i<=N; i++) {
cin >> v[i] >> u[i];
vsum += v[i];
usum += u[i];
}
adj.clear();
adj.resize(N+4);
int ext = N+1, sour = N+2, sink = N+3;
for(int i=1; i<=N; i++) {
edge(sour, i, v[i], 0);
edge(i, sink, u[i], 0);
edge(i, ext, INT_MAX, Y);
edge(ext, i, INT_MAX, X);
for(int j=1; j<=N; j++)
if(i != j) edge(i, j, INT_MAX, abs(i-j)*Z);
}
int ans = 0;
if(vsum > usum) ans += (vsum - usum) * Y;
else if(vsum < usum) ans += (usum - vsum) * X;
maxf = 0, minc = 0;
mcmf(sour, sink);
ans += minc;
cout << ans << "\n";
}
백준 BOJ 17506번 : 주때의 자소서 쓰기
문제 난이도 : Platinum II
알고리즘 분류 : MCMF (최소 비용 최대 유량)
처음에는 이렇게 접근했다.

그런데 A, B, C 각각에 최소 하나 이상의 소재는 배정을 받아야 한다는 조건이 있다.
이를 처리해주기 위해서는 아주 낮은 비용으로 유량을 1씩 흘려줘서 무조건 흘러주게 하는 방법이 있는데, 그렇게 하기 위해서는 그래프를 좌우로 뒤집어주어야 한다. (A, B, C가 왼쪽으로 오도록)
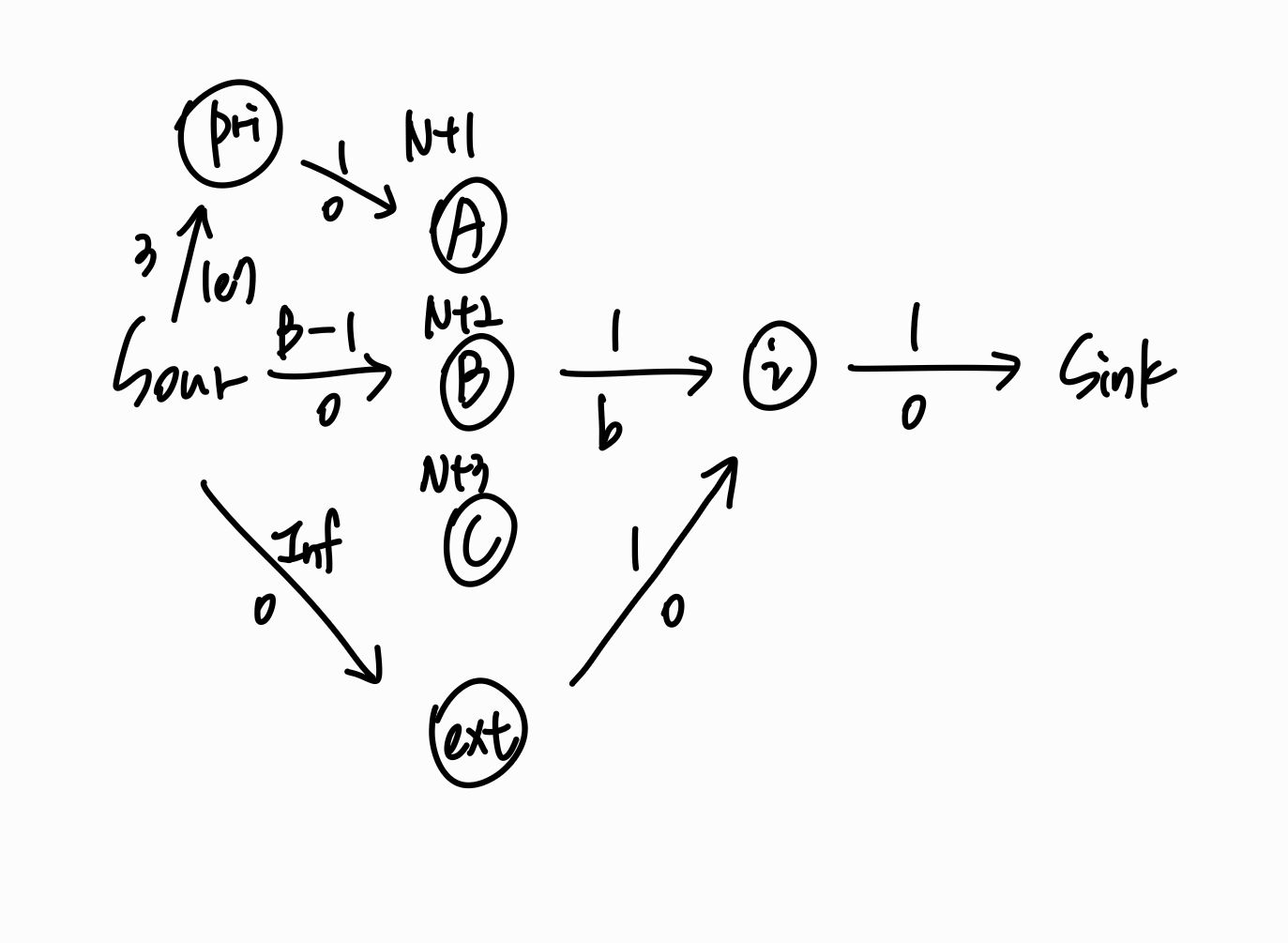
그러면 이렇게 되고, -1e7 정도의 값으로 pri 노드에 유량을 흘려주면, 최소 비용으로 유량이 흐르므로 pri 노드의 3의 유량은 무조건 A, B, C 각각에 1씩 흐르게 된다.
이들이 우선적으로 배정이 되고, 그 다음 나머지 유량들이 흐르므로 원하는 결과를 얻을 수 있게 된다.
마지막에는 3e7을 더해준 뒤 마이너스 붙여서 답을 구해주면 된다.
#include <bits/stdc++.h>
#define int long long
using namespace std;
struct MCMF {
// referred to the jhnah917's implementation (purpose of study)
struct se { int num, cap, sco, ord; };
vector<vector<se>> adj;
void edge(int a, int b, int c, int d) {
adj[a].push_back({b, c, d, adj[b].size()});
adj[b].push_back({a, 0, -d, adj[a].size()-1});
}
int sour, sink;
vector<int> tco, idx;
vector<bool> chk;
int dfs(int x, int flo) {
chk[x] = true;
if(x == sink) return flo;
for(; idx[x] < adj[x].size(); idx[x]++) {
se &ad = adj[x][idx[x]];
if(chk[ad.num] || tco[x] + ad.sco != tco[ad.num] || ad.cap == 0) continue;
int ret = dfs(ad.num, min(flo, ad.cap));
if(ret == 0) continue;
ad.cap -= ret;
adj[ad.num][ad.ord].cap += ret;
return ret;
}
return 0;
}
pair<int, int> mcmf(int sour_, int sink_) {
sour = sour_, sink = sink_;
int minc = 0, maxf = 0;
tco.resize(adj.size(), INT_MAX);
tco[sour] = 0;
queue<int> q;
q.push(sour);
vector<bool> inq(adj.size());
inq[sour] = true;
while(!q.empty()) {
int x = q.front();
q.pop(); inq[x] = false;
for(int i=0; i<adj[x].size(); i++) {
int y = adj[x][i].num;
int cap = adj[x][i].cap;
int sco = adj[x][i].sco;
if(cap <= 0 || tco[x] + sco >= tco[y]) continue;
tco[y] = tco[x] + sco;
if(inq[y]) continue;
q.push(y);
inq[y] = true;
}
}
while(true) {
chk.clear(); chk.resize(adj.size());
idx.clear(); idx.resize(adj.size());
while(true) {
int cur = dfs(sour, INT_MAX);
if(cur == 0) break;
minc += tco[sink] * cur;
maxf += cur;
chk.clear(); chk.resize(adj.size());
}
int Min = INT_MAX;
for(int i=0; i<adj.size(); i++) {
if(!chk[i]) continue;
for(int j=0; j<adj[i].size(); j++) {
int x = adj[i][j].num;
int cap = adj[i][j].cap;
int sco = adj[i][j].sco;
if(cap > 0 && !chk[x]) Min = min(Min, tco[i] + sco - tco[x]);
}
}
if(Min == INT_MAX) break;
for(int i=0; i<adj.size(); i++)
if(!chk[i]) tco[i] += Min;
}
return {minc, maxf};
}
};
main() {
ios_base::sync_with_stdio(false);
cin.tie(NULL), cout.tie(NULL);
int N; cin >> N;
MCMF f;
int S = N+8;
f.adj.resize(S);
int sour = S-1, sink = S-2, pri = S-3, ext = S-4;
f.edge(sour, pri, 3, -1e7);
f.edge(sour, ext, INT_MAX, 0);
for(int i=1; i<=3; i++) {
int x; cin >> x;
f.edge(sour, N+i, x-1, 0);
f.edge(pri, N+i, 1, 0);
}
for(int i=1; i<=N; i++) {
for(int j=1; j<=3; j++) {
int x; cin >> x;
f.edge(N+j, i, 1, -x);
}
f.edge(ext, i, 1, 0);
f.edge(i, sink, 1, 0);
}
pair<int, int> mcmf = f.mcmf(sour, sink);
int minc = mcmf.first;
int maxf = mcmf.second;
int ans = -(minc + 1e7 * 3);
cout << ans << "\n";
}
백준 BOJ 7154번 : Job Postings
문제 난이도 : Platinum III
알고리즘 분류 : MCMF (최소 비용 최대 유량)
이 문제는 어렵지는 않은데 누가 질문글을 올렸고 구글링해봐도 풀이가 없길래 간단하게 그래프와 풀이 코드만 첨부한다.

#include <bits/stdc++.h>
#define int long long
using namespace std;
struct se {
int num, cap, sco, ord;
se(int num, int cap, int sco, int ord) : num(num), cap(cap), sco(sco), ord(ord) {}
};
vector<vector<se>> adj;
int maxf, minc;
void edge(int a, int b, int c, int d) {
adj[a].emplace_back(b, c, d, adj[b].size());
adj[b].emplace_back(a, 0, -d, adj[a].size()-1);
}
void mcmf(int sour, int sink) {
while(true) {
vector<int> pre(adj.size(), -1), idx(adj.size(), -1);
vector<int> tco(adj.size(), INT_MAX);
tco[sour] = 0;
queue<int> q;
q.push(sour);
vector<bool> inq(adj.size());
inq[sour] = true;
while(!q.empty()) {
int x = q.front();
q.pop();
inq[x] = false;
for(int i=0; i<adj[x].size(); i++) {
int y = adj[x][i].num;
int cap = adj[x][i].cap;
int sco = adj[x][i].sco;
if(cap <= 0 || tco[x] + sco >= tco[y]) continue;
tco[y] = tco[x] + sco;
pre[y] = x;
idx[y] = i;
if(inq[y]) continue;
q.push(y);
inq[y] = true;
}
}
if(pre[sink] == -1) break;
int sfl = INT_MAX;
for(int i=sink; i!=sour; i=pre[i]) {
int a = pre[i], b = idx[i];
sfl = min(sfl, adj[a][b].cap);
}
for(int i=sink; i!=sour; i=pre[i]) {
int a = pre[i], b = idx[i];
adj[a][b].cap -= sfl;
adj[i][adj[a][b].ord].cap += sfl;
minc += sfl * adj[a][b].sco;
}
maxf += sfl;
}
}
main() {
ios_base::sync_with_stdio(false);
cin.tie(NULL), cout.tie(NULL);
while(true) {
int N, M; cin >> M >> N;
if(N == 0 && M == 0) break;
adj.clear();
adj.resize(N+M+3);
int sour = N+M+1, sink = N+M+2;
for(int i=1; i<=M; i++) {
int x; cin >> x;
edge(N+i, sink, x, 0);
}
for(int i=1; i<=N; i++) {
edge(sour, i, 1, 0);
int a; cin >> a;
for(int j=0; j<4; j++) {
int b; cin >> b;
edge(i, N+b+1, 1, -(a*4-j));
}
}
maxf = minc = 0;
mcmf(sour, sink);
cout << -minc << "\n";
}
}
백준 BOJ 1650번 : 지민이의 테러 Season II
문제 난이도 : Platinum III
알고리즘 분류 : MCMF (최소 비용 최대 유량)
같은 길을 두 번 지나가지 않되 1번 노드에서 N번 노드 사이를 왕복하는 최소 비용을 구하는 문제이다.
간선의 방향이 양방향인 경우 반대로 갈 때 마이너스 비용 처리를 하기 애매하므로 노드를 분할하여 in, out을 따로 처리해주면 된다.
그리고 이 문제에서는 왕복 비용을 구하라고 하였으므로 유량을 2만큼 흘려주면 된다.
#include <bits/stdc++.h>
#define int long long
using namespace std;
struct se {
int num, cap, sco, ord;
se(int num, int cap, int sco, int ord) : num(num), cap(cap), sco(sco), ord(ord) {}
};
vector<vector<se>> adj;
int maxf, minc;
void edge(int a, int b, int c, int d) {
adj[a].emplace_back(b, c, d, adj[b].size());
adj[b].emplace_back(a, 0, -d, adj[a].size()-1);
}
void mcmf(int sour, int sink) {
while(true) {
vector<int> pre(adj.size(), -1), idx(adj.size(), -1);
vector<int> tco(adj.size(), INT_MAX);
tco[sour] = 0;
queue<int> q;
q.push(sour);
vector<bool> inq(adj.size());
inq[sour] = true;
while(!q.empty()) {
int x = q.front();
q.pop();
inq[x] = false;
for(int i=0; i<adj[x].size(); i++) {
int y = adj[x][i].num;
int cap = adj[x][i].cap;
int sco = adj[x][i].sco;
if(cap <= 0 || tco[x] + sco >= tco[y]) continue;
tco[y] = tco[x] + sco;
pre[y] = x;
idx[y] = i;
if(inq[y]) continue;
q.push(y);
inq[y] = true;
}
}
if(pre[sink] == -1) break;
int sfl = INT_MAX;
for(int i=sink; i!=sour; i=pre[i]) {
int a = pre[i], b = idx[i];
sfl = min(sfl, adj[a][b].cap);
}
for(int i=sink; i!=sour; i=pre[i]) {
int a = pre[i], b = idx[i];
adj[a][b].cap -= sfl;
adj[i][adj[a][b].ord].cap += sfl;
minc += sfl * adj[a][b].sco;
}
maxf += sfl;
}
}
main() {
ios_base::sync_with_stdio(false);
cin.tie(NULL), cout.tie(NULL);
int N, M; cin >> N >> M;
adj.clear();
adj.resize(N*2 + 3);
int sour = N*2 + 1, sink = N*2 + 2;
edge(sour, 1, 2, 0);
edge(N+N, sink, 2, 0);
for(int i=1; i<=N; i++) edge(i, N+i, INT_MAX, 0);
while(M--) {
int a, b, c; cin >> a >> b >> c;
edge(N+a, b, 1, c);
edge(N+b, a, 1 ,c);
}
maxf = 0, minc = 0;
mcmf(sour, sink);
cout << minc << "\n";
}
'알고리즘 > 알고리즘 공부 내용 정리' 카테고리의 다른 글
| 12월 알고리즘 공부 : 퍼시스턴트 세그먼트 트리, 머지 소트 트리, 오일러 회로 등 (1) | 2022.12.14 |
|---|---|
| 백준 BOJ 2-SAT 알고리즘 심화 문제 풀이 (0) | 2022.11.27 |
| 11월 알고리즘 공부 : 최소 외접원/구, 가장 가까운 두 점, 번사이드 보조정리 등 (1) | 2022.11.22 |
| 백준 BOJ 17030번 : Cow Dating 풀이 (Diamond V, 투 포인터) (0) | 2022.11.12 |
| 백준 BOJ 24486번 : Counting Haybales 풀이 (Diamond II, DP) (0) | 2022.11.10 |