백준 BOJ 12987번 : Matrix Again
문제 난이도 : Gold II
알고리즘 분류 : 분할 정복을 이용한 거듭제곱
주어진 행렬 A에 대해, S = A + A^2 + ... + A^K를 구하는 문제이다.
단일 행렬에 대한 거듭제곱은 N^2 log K 시간에 구할 수 있으나, 식 S의 경우에는 그러한 방식을 쓰더라도 결국 각 항을 따로 구하면 시간 복잡도가 늘어난다.
따라서 이 문제에서는 점화식을 사용하여 분할 정복으로 문제를 풀어주어야 되는데, 점화식은 다음과 같다.

위와 같이 점화식을 세우면 K를 계속해서 2로 나눠가면서 log 시간 복잡도로 식의 값을 구할 수 있다.
이 때 ( i ) 케이스의 A^(K/2)는 분할 정복을 이용한 거듭제곱 알고리즘을 사용하여 log(K) 시간에 구해준다.
구현해야 하는 함수가 많아서 복잡할 수 있지만, 어떤 부분을 나눠야 하는지 잘 생각하면서 하면 구현할 수 있을 것이다.
참고로 시간 초과가 발생할 수 있는데, 아래 코드의 mul 함수에서 mod 처리를 하는 과정이 요인이 될 수 있다.
예를 들어 w[i][j] = (w[i][j] + v[i][k] * u[k][j]) % mod와 같이 식을 세울 경우, 단일 덧셈마다 mod 처리를 하여 N^3번의 나눗셈이 발생하는데, 이를 줄이기 위해 k에 대한 루프가 끝난 이후에 한 번만 나누도록 해주면 시간을 많이 단축시킬 수 있다.
#include <bits/stdc++.h>
#define int long long
using namespace std;
typedef vector<vector<int>> mat;
int N, K, mod;
mat mul(mat v, mat u) {
mat w(N, vector<int>(N));
for(int i=0; i<N; i++)
for(int j=0; j<N; j++) {
for(int k=0; k<N; k++) w[i][j] += v[i][k] * u[k][j];
w[i][j] %= mod;
}
return w;
}
mat fpow(mat ba, int K) {
mat v(N, vector<int>(N));
for(int i=0; i<N; i++) v[i][i] = 1;
while(K > 0) {
if(K % 2 == 1) v = mul(v, ba);
ba = mul(ba, ba);
K /= 2;
}
return v;
}
mat f(mat ba, int K) {
if(K == 1) return ba;
if(K % 2 == 0) {
mat v = f(ba, K/2);
mat u = fpow(ba, K/2);
for(int i=0; i<N; i++) u[i][i] = (u[i][i] + 1) % mod;
mat w = mul(v, u);
return w;
}
if(K % 2 == 1) {
mat v = f(ba, K-1);
mat u = fpow(ba, K);
for(int i=0; i<N; i++)
for(int j=0; j<N; j++)
v[i][j] = (v[i][j] + u[i][j]) % mod;
return v;
}
}
main() {
ios_base::sync_with_stdio(false);
cin.tie(NULL), cout.tie(NULL);
cin >> N >> K >> mod;
mat v(N, vector<int>(N));
for(int i=0; i<N; i++)
for(int j=0; j<N; j++) {
cin >> v[i][j];
v[i][j] = ((v[i][j] % mod) + mod) % mod;
}
mat ans = f(v, K);
for(int i=0; i<N; i++) {
for(int j=0; j<N; j++) cout << ans[i][j] << " ";
cout << "\n";
}
}
백준 BOJ 13246번 : 행렬 제곱의 합
문제 난이도 : Gold II
알고리즘 분류 : 분할 정복을 이용한 거듭제곱
위의 문제와 동일한 문제이다.
풀이도 같으나, mod 부분만 변수가 아닌 고정값 1,000으로 수정해서 풀이해주면 된다.
중복되는 부분이 많아 풀이 코드는 아래의 접은 글에 정리해두었다.
#include <bits/stdc++.h>
#define int long long
using namespace std;
typedef vector<vector<int>> mat;
int N, K, mod = 1e3;
mat mul(mat v, mat u) {
mat w(N, vector<int>(N));
for(int i=0; i<N; i++)
for(int j=0; j<N; j++) {
for(int k=0; k<N; k++) w[i][j] += v[i][k] * u[k][j];
w[i][j] %= mod;
}
return w;
}
mat fpow(mat ba, int K) {
mat v(N, vector<int>(N));
for(int i=0; i<N; i++) v[i][i] = 1;
while(K > 0) {
if(K % 2 == 1) v = mul(v, ba);
ba = mul(ba, ba);
K /= 2;
}
return v;
}
mat f(mat ba, int K) {
if(K == 1) return ba;
if(K % 2 == 0) {
mat v = f(ba, K/2);
mat u = fpow(ba, K/2);
for(int i=0; i<N; i++) u[i][i] = (u[i][i] + 1) % mod;
mat w = mul(v, u);
return w;
}
if(K % 2 == 1) {
mat v = f(ba, K-1);
mat u = fpow(ba, K);
for(int i=0; i<N; i++)
for(int j=0; j<N; j++)
v[i][j] = (v[i][j] + u[i][j]) % mod;
return v;
}
}
main() {
ios_base::sync_with_stdio(false);
cin.tie(NULL), cout.tie(NULL);
cin >> N >> K;
mat v(N, vector<int>(N));
for(int i=0; i<N; i++)
for(int j=0; j<N; j++) {
cin >> v[i][j];
v[i][j] = ((v[i][j] % mod) + mod) % mod;
}
mat ans = f(v, K);
for(int i=0; i<N; i++) {
for(int j=0; j<N; j++) cout << ans[i][j] << " ";
cout << "\n";
}
}
백준 BOJ 15712번 : 등비수열
문제 난이도 : Gold II
알고리즘 분류 : 분할 정복을 이용한 거듭제곱
첫 항이 a, 공비가 r, 항의 수가 N인 등비수열의 합을 mod로 나눈 나머지를 구하는 문제이다.
만약 mod 값이 소수였다면, 등비수열의 합 공식을 사용한 뒤 페르마의 소정리를 사용하여 아주 간단하게 풀이할 수 있다.
그러나 여기서는 그러한 조건이 없으므로, 직접 항들을 계산하는 방식을 생각해보아야 한다.

위에서 사용한 분할 정복의 방식을 사용하면, 항의 개수의 log 값에 비례한 수행 시간으로 답을 얻을 수 있다.
구현 자체도 거의 비슷하고, 행렬 대신 정수에 대한 연산이므로 비교적 간단하게 풀이할 수 있다.
참고로 위에서 풀이한 방식대로 하면 N = 1인 경우 무한 루프를 돌게 된다.
따라서 N = 1인 경우 a % mod를 답으로 출력하여 예외 처리를 해주도록 한다.
#include <bits/stdc++.h>
#define int long long
using namespace std;
int a, r, N, mod;
int fpow(int ba, int ex) {
int val = 1;
while(ex > 0) {
if(ex % 2 == 1) val = (val * ba) % mod;
ba = (ba * ba) % mod;
ex /= 2;
}
return val;
}
int f(int ba, int ex) {
if(ex == 1) return ba;
if(ex % 2 == 0) {
int a = f(ba, ex/2);
int b = fpow(ba, ex/2);
return (a * (b + 1)) % mod;
}
if(ex % 2 == 1) {
int a = f(ba, ex-1);
int b = fpow(ba, ex);
return (a + b) % mod;
}
}
main() {
ios_base::sync_with_stdio(false);
cin.tie(NULL), cout.tie(NULL);
cin >> a >> r >> N >> mod;
if(N == 1) {
cout << a % mod << "\n";
return 0;
}
int ans = f(r % mod, N-1);
ans = ((ans + 1) * a) % mod;
cout << ans << "\n";
}
백준 BOJ 12850번 : 본대 산책2
문제 난이도 : Gold I
알고리즘 분류 : 분할 정복을 이용한 거듭제곱

위와 같은 그래프가 주어질 때, 정보과학관에서 출발하여 N번 이동 후 다시 정보과학관으로 돌아오는 경우의 수를 구하는 문제이다.
8 x 8 크기의 인접 그래프를 만들어 준 뒤, 이를 N 제곱했을 때 얻어지는 행렬의 원소 a_ij는 i번 노드에서 인접한 노드로 N번 이동하여 j번 노드에 도달하는 경우의 수가 된다.
왜냐하면 예를 들어 행렬을 2번 곱, 즉 제곱했다면 a_ij는 모든 k에 대한 a_ik * a_kj이므로, i에서 k로 이동하는 경우의 수에 k에서 j로 이동하는 경우의 수의 합인 것이다.
이러한 방식을 귀납적으로 생각해보면 인접 행렬을 N 제곱해주면 결국 a_ij는 i번 노드에서 인접한 노드로 N번 이동하여 j번 노드에 도달하는 경우의 수가 된다.
따라서 주어진 그래프의 번호만 편한대로 적절히 매겨서 빠른 거듭 제곱을 해준 뒤, 정보과학관에서 정보과학관으로 이동하는 것이므로 해당하는 원소를 답으로 얻어주면 된다.
#include <bits/stdc++.h>
#define int long long
using namespace std;
typedef vector<vector<int>> mat;
int N = 8, ex, mod = 1e9 + 7;
mat f(mat& v, mat& u) {
mat w(N, vector<int>(N));
for(int i=0; i<N; i++)
for(int j=0; j<N; j++)
for(int k=0; k<N; k++)
w[i][j] = (w[i][j] + v[i][k] * u[k][j]) % mod;
return w;
}
main() {
ios_base::sync_with_stdio(false);
cin.tie(NULL), cout.tie(NULL);
cin >> ex;
mat v(N, vector<int>(N));
for(int i=0; i<N; i++) v[i][i] = 1;
mat ba(N, vector<int>(N));
ba = {{0, 1, 1, 0, 0, 0, 0, 0},
{1, 0, 1, 1, 0, 0, 0, 0},
{1, 1, 0, 1, 1, 0, 0, 0},
{0, 1, 1, 0, 1, 1, 0, 0},
{0, 0, 1, 1, 0, 1, 0, 1},
{0, 0, 0, 1, 1, 0, 1, 0},
{0, 0, 0, 0, 0, 1, 0, 1},
{0, 0, 0, 0, 1, 0, 1, 0}};
while(ex > 0) {
if(ex % 2 == 1) v = f(v, ba);
ba = f(ba, ba);
ex /= 2;
}
cout << v[0][0] << "\n";
}
백준 BOJ 14289번 : 본대 산책3
문제 난이도 : Gold I
알고리즘 분류 : 그래프 이론, 분할 정복을 이용한 거듭제곱
위의 문제와 동일하나, 노드의 수와 그래프의 간선들, 그리고 시간을 변수로 주는 문제이다.
이번에는 인접 행렬을 변수로 받아주면 된다.
N x N 크기의 인접 행렬을 만들고, a번 노드와 b번 사이에 직접적인 간선이 존재한다면 v[a][b] = v[b][a] = 1로 설정해주면 된다.
원래라면 ++ 연산을 해주어야겠지만 이 문제에서는 같은 간선이 두 개 이상 나오지 않는다고 보장해주었으므로 위와 같이 작성해도 된다.
나머지 구현은 본대 산책2 문제와 동일하다.
#include <bits/stdc++.h>
#define int long long
using namespace std;
typedef vector<vector<int>> mat;
int N, M, ex, mod = 1e9 + 7;
mat f(mat& v, mat& u) {
mat w(N, vector<int>(N));
for(int i=0; i<N; i++)
for(int j=0; j<N; j++)
for(int k=0; k<N; k++)
w[i][j] = (w[i][j] + v[i][k] * u[k][j]) % mod;
return w;
}
main() {
ios_base::sync_with_stdio(false);
cin.tie(NULL), cout.tie(NULL);
cin >> N >> M;
mat v(N, vector<int>(N));
for(int i=0; i<N; i++) v[i][i] = 1;
mat ba(N, vector<int>(N));
while(M--) {
int a, b; cin >> a >> b;
ba[a-1][b-1] = ba[b-1][a-1] = 1;
}
cin >> ex;
while(ex > 0) {
if(ex % 2 == 1) v = f(v, ba);
ba = f(ba, ba);
ex /= 2;
}
cout << v[0][0] << "\n";
}
백준 BOJ 15824번 : 너 봄에는 캡사이신이 맛있단다
문제 난이도 : Gold II
알고리즘 분류 : 분할 정복을 이용한 거듭제곱
N개의 수 중에서 부분 수열을 골랐을 때, 그 부분 수열의 최댓값에서 최솟값을 뺀 값이 주헌고통지수라고 할 때, 가능한 모든 조합의 주헌고통지수의 합을 구하는 문제이다.
문제에서 정의된 주헌고통지수는 오직 부분 수열의 최대/최소에만 영향이 있으므로, 수열을 정렬한 뒤 생각해도 답에는 영향이 없다. 따라서 우선 수열을 정렬하고 생각해보자.
그 다음 최솟값이 l번째이고, 최댓값이 r번째인 부분 수열을 생각해보면 [v_l , ... , v_r]인 수열의 종류는 l+1, ... , r-1번째 수를 각각 선택 또는 선택하지 않을 수 있으므로 2^(r - l - 1)가지이고 주헌고통지수의 합은 2^(r - l - 1) x (v_r - v_l)이다.
이제 r - l이 같은 값들에 대해 모든 조합들을 생각해보자.
예를 들어 r - l = 1인 조합들에 대해서 생각해보면, 이들의 합은 2^(1 - 1) x (v_2 - v_1 + v_3 - v_2 + ... + v_N - v_(N-1)) = v_N - v_1이다.
r - l = 2인 조합들에 대해 생각해보면, 이들의 합은 2^(2 - 1) x (v_3 - v_1 + v_4 - v_2 + ... + v_N - v_(N-2)) = 2 x (v_N + v_(N-1) - v_2 - v_1)이다.
규칙을 보면 2^(r - l - 1) x (v_N + ... + v_(N - (r - l + 1)) - (v_1 + v_2 + ... + v_(r - l))이 된다.
이제 이 식을 r - l 으로 나올 수 있는 값인 1 ~ N-1에 대해 모두 더해주면 된다.
식을 잘 정리하면 풀이 코드를 아래와 같이 정리할 수 있는데, 이는 아래의 내 풀이를 직접 참고하는 것을 추천한다. (누적 합을 사용하면 조금 간단하게 풀이할 수 있다.)
참고로 모듈로 연산을 잘못 할 경우 음수가 나오거나 하여 WA를 받을 수 있다.
모듈로는 정렬이 끝나고, 각 연산에 대해 v_r - v_l을 구한 뒤부터 해주도록 하자.
#include <bits/stdc++.h>
#define int long long
using namespace std;
main() {
ios_base::sync_with_stdio(false);
cin.tie(NULL), cout.tie(NULL);
int N; cin >> N;
int mod = 1e9 + 7;
vector<int> v(N);
for(int i=0; i<N; i++) cin >> v[i];
sort(v.begin(), v.end());
vector<int> u(N); u[0] = v[0];
for(int i=1; i<N; i++) u[i] = u[i-1] + v[i];
vector<int> w(N); w[N-1] = v[N-1];
for(int i=N-2; i>=0; i--) w[i] = w[i+1] + v[i];
int ans = 0;
for(int i=0; i<N; i++) {
int val = (w[N-1-i] - u[i]) % mod, ba = 2, ex = i;
while(ex > 0) {
if(ex % 2 == 1) val = (val * ba) % mod;
ba = (ba * ba) % mod;
ex /= 2;
}
ans = (ans + val) % mod;
}
cout << ans << "\n";
}
백준 BOJ 13075번 : Fibonacci Sequence
문제 난이도 : Gold II
알고리즘 분류 : 분할 정복을 이용한 거듭제곱
피보나치 수열의 N번째 항을 구하는 문제이다. (mod 1e9)
단순히 행렬의 거듭제곱을 이용하여 답을 구해주면 된다.
이전에 많이 다루었던 문제들이므로 설명은 생략하며, 역시 접은 글에 풀이 코드를 첨부한다.
#include <bits/stdc++.h>
#define int long long
using namespace std;
typedef vector<vector<int>> mat;
int mod = 1e9;
mat f(mat& v, mat& u) {
int N = 2;
mat w(N, vector<int>(N));
for(int i=0; i<v.size(); i++)
for(int j=0; j<u[0].size(); j++)
for(int k=0; k<v[0].size(); k++)
w[i][j] = (w[i][j] + v[i][k] * u[k][j]) % mod;
return w;
}
main() {
ios_base::sync_with_stdio(false);
cin.tie(NULL), cout.tie(NULL);
int T; cin >> T;
while(T--) {
int N; cin >> N;
mat mul(2, vector<int>(2));
for(int i=0; i<2; i++) mul[i][i] = 1;
mat ba(2, vector<int>(2));
ba = {{1, 1}, {1, 0}};
while(N > 0) {
if(N % 2 == 1) mul = f(mul, ba);
ba = f(ba, ba);
N /= 2;
}
cout << mul[0][1] << "\n";
}
}
백준 BOJ 2086번 : 피보나치 수의 합
문제 난이도 : Gold I
알고리즘 분류 : 분할 정복을 이용한 거듭제곱
피보나치 수열의 1항을 1, 2항을 1이라고 할 때, a, b에 대해 a번째부터 b번째 피보나치 수의 합을 구하는 문제이다.
먼저 다음 코드로 피보나치 수열과 1 ~ i번째 항의 합을 두 줄에 걸쳐 나타내어보면 다음과 같다.
코드는 접은 글에 있다. (정답 코드 아님)
#include <bits/stdc++.h>
#define int long long
using namespace std;
main() {
ios_base::sync_with_stdio(false);
cin.tie(NULL), cout.tie(NULL);
int N; cin >> N;
vector<int> v(N+1);
v[1] = 1;
for(int i=2; i<=N; i++) v[i] = v[i-1] + v[i-2];
for(int i=1; i<=N; i++) printf("%5d", v[i]);
printf("\n");
for(int i=1; i<=N; i++) {
v[i] += v[i-1];
printf("%5d", v[i]);
}
}
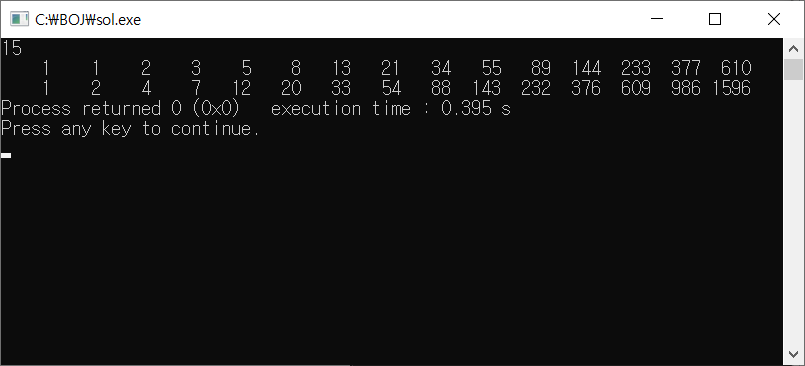
규칙성을 찾아보면, 1 ~ N번째 피보나치 수열의 합은 N+2번째 피보나치 수 - 1임을 알 수 있다.
따라서 분할 정복을 이용한 거듭제곱을 이용하여 (b+2번째 피보나치 수 - 1) - (a+2-1번째 피보나치 수 - 1) = (b+2번째 피보나치 수 ) - (a+1번째 피보나치 수)를 답으로 구해주면 된다.
이 때 모듈로에 의해 뒤의 수가 더 클 수도 있으므로, 모듈로를 한 번 더한 뒤 모듈로 처리를 해주면 된다.
#include <bits/stdc++.h>
#define int long long
using namespace std;
typedef vector<vector<int>> mat;
int mod = 1e9;
mat f(mat& v, mat& u) {
int N = 2;
mat w(N, vector<int>(N));
for(int i=0; i<v.size(); i++)
for(int j=0; j<u[0].size(); j++)
for(int k=0; k<v[0].size(); k++)
w[i][j] = (w[i][j] + v[i][k] * u[k][j]) % mod;
return w;
}
main() {
ios_base::sync_with_stdio(false);
cin.tie(NULL), cout.tie(NULL);
vector<int> v(2);
for(int i=0; i<2; i++) cin >> v[i];
v[0] += 2 - 1;
v[1] += 2;
vector<int> u(2);
for(int t=0; t<2; t++) {
int N = v[t];
mat mul(2, vector<int>(2));
for(int i=0; i<2; i++) mul[i][i] = 1;
mat ba(2, vector<int>(2));
ba = {{1, 1}, {1, 0}};
while(N > 0) {
if(N % 2 == 1) mul = f(mul, ba);
ba = f(ba, ba);
N /= 2;
}
u[t] = mul[0][1];
}
int ans = (u[1] - u[0] + mod) % mod;
cout << ans << "\n";
}
백준 BOJ 11238번 : Fibo
문제 난이도 : Gold I
알고리즘 분류 : 정수론, 분할 정복을 이용한 거듭제곱
10억 이하의 a 또는 b에 대해 a번째 피보나치 수와 b번째 피보나치 수의 최대공약수를 구하는 문제이다.
우리는 분할 정복을 이용한 거듭제곱으로 a 또는 b번째 피보나치 수를 구할 수는 있으나, 모듈로 연산을 해버리면 gcd 값이 달라지므로 다른 방법을 생각해야 한다.
피보나치 수의 성질 중 하나로 a번째 피보나치 수와 b번째 피보나치 수의 최대공약수는 (a와 b의 최대공약수)번째 피보나치수임을 만족한다.
증명 과정을 읽어봤는데 a와 b에 대해 유클리드 호제법을 사용함과 동시에 몇 가지 Lemma들을 사용하여 증명한다.
이러한 성질은 분명 중요하지만, 이런 증명 과정 자체가 PS에서 자주 사용되지는 않는다고 생각하기에 여기서는 증명 과정 없이 이러한 성질을 활용하여 풀이한 코드만 첨부한다.
#include <bits/stdc++.h>
#define int long long
using namespace std;
typedef vector<vector<int>> mat;
int mod = 1e9 + 7;
mat f(mat& v, mat& u) {
int N = 2;
mat w(N, vector<int>(N));
for(int i=0; i<v.size(); i++)
for(int j=0; j<u[0].size(); j++)
for(int k=0; k<v[0].size(); k++)
w[i][j] = (w[i][j] + v[i][k] * u[k][j]) % mod;
return w;
}
main() {
ios_base::sync_with_stdio(false);
cin.tie(NULL), cout.tie(NULL);
int T; cin >> T;
while(T--) {
int a, b; cin >> a >> b;
int N = __gcd(a, b);
mat mul(2, vector<int>(2));
for(int i=0; i<2; i++) mul[i][i] = 1;
mat ba(2, vector<int>(2));
ba = {{1, 1}, {1, 0}};
while(N > 0) {
if(N % 2 == 1) mul = f(mul, ba);
ba = f(ba, ba);
N /= 2;
}
cout << mul[0][1] << "\n";
}
}
백준 BOJ 11778번 : 피보나치 수와 최대공약수
문제 난이도 : Gold I
알고리즘 분류 : 정수론, 분할 정복을 이용한 거듭제곱
위의 문제와 동일한 문제이다. (문제 언어만 다르다.)
같은 방식으로 풀이해주되, 테스트케이스 처리부만 제거해주면 된다.
중복 문제이므로 접은 글에 풀이 코드를 첨부한다.
#include <bits/stdc++.h>
#define int long long
using namespace std;
typedef vector<vector<int>> mat;
int mod = 1e9 + 7;
mat f(mat& v, mat& u) {
int N = 2;
mat w(N, vector<int>(N));
for(int i=0; i<v.size(); i++)
for(int j=0; j<u[0].size(); j++)
for(int k=0; k<v[0].size(); k++)
w[i][j] = (w[i][j] + v[i][k] * u[k][j]) % mod;
return w;
}
main() {
ios_base::sync_with_stdio(false);
cin.tie(NULL), cout.tie(NULL);
int a, b; cin >> a >> b;
int N = __gcd(a, b);
mat mul(2, vector<int>(2));
for(int i=0; i<2; i++) mul[i][i] = 1;
mat ba(2, vector<int>(2));
ba = {{1, 1}, {1, 0}};
while(N > 0) {
if(N % 2 == 1) mul = f(mul, ba);
ba = f(ba, ba);
N /= 2;
}
cout << mul[0][1] << "\n";
}
백준 BOJ 16134번 : 조합 (Combination)
문제 난이도 : Gold I
알고리즘 분류 : 분할 정복을 이용한 거듭제곱
N C M mod 1e9 + 7을 구하는 문제이다. 이 때 0 ≤ M ≤ N ≤ 1,000,000이다.
단순히 페르마의 소정리를 활용하여 mod 값을 구해주면 된다.
N! mod 1e9 + 7은 O(N)에 구할 수 있고, 분모의 경우에는 하나의 분모당 log(1e9 + 7) 시간에 수행할 수 있으므로, O(M log mod) 시간에 풀이 가능하다.
#include <bits/stdc++.h>
#define int long long
using namespace std;
main() {
ios_base::sync_with_stdio(false);
cin.tie(NULL), cout.tie(NULL);
int N, M; cin >> N >> M;
M = min(M, N - M);
int ans = 1, mod = 1e9 + 7;
for(int i=N; i>=N-M+1; i--) ans = (ans * i) % mod;
for(int i=1; i<=M; i++) {
int ba = i, ex = mod - 2;
while(ex > 0) {
if(ex % 2 == 1) ans = (ans * ba) % mod;
ba = (ba * ba) % mod;
ex /= 2;
}
}
cout << ans << "\n";
}
'알고리즘 > 알고리즘 공부 내용 정리' 카테고리의 다른 글
| 백준 BOJ 스위핑, 값/좌표 압축 알고리즘 문제 풀이 모음 220819 (0) | 2022.08.19 |
|---|---|
| 백준 BOJ 문제 풀이 모음 : 그래프와 인접 행렬의 활용 220818 (0) | 2022.08.18 |
| 백준 BOJ 분할 정복을 이용한 거듭제곱 문제 풀이 모음 220816 (0) | 2022.08.16 |
| 백준 BOJ 최소 스패닝 트리 (MST) 문제 풀이 모음 220813 (0) | 2022.08.13 |
| 백준 BOJ Gold 난이도 구현 외 다양한 문제들 풀이 220812 (0) | 2022.08.12 |