백준 BOJ 17199번 : Milk Factory
문제 난이도 : Silver I
알고리즘 분류 : DFS
그래프가 주어질 때 모든 지점에서 모일 수 있는 어느 한 점이 존재하는지를 구하고 존재한다면 그러한 가장 작은 노드 번호를 구하는 문제이다.
노드 수가 최대 100개밖에 되지 않으므로, 모든 노드에 대해 다른 모든 노드에서 방문이 가능한지 검사해주면 된다.
즉, DFS를 대략 N^2회 수행해주어 체크해주면 된다.
#include <bits/stdc++.h>
#define int long long
using namespace std;
vector<vector<int>> adj;
vector<bool> vis;
void f(int x) {
vis[x] = true;
for(int i=0; i<adj[x].size(); i++) {
int y = adj[x][i];
if(!vis[y]) f(y);
}
}
main() {
ios_base::sync_with_stdio(false);
cin.tie(NULL), cout.tie(NULL);
int N; cin >> N;
adj.resize(N+1);
for(int i=0; i<N-1; i++) {
int a, b; cin >> a >> b;
adj[a].push_back(b);
}
for(int i=1; i<=N; i++) {
bool check = true;
for(int j=1; j<=N; j++) {
vis.clear();
vis.resize(N+1);
f(j);
if(!vis[i]) check = false;
}
if(check) {
cout << i << "\n";
return 0;
}
}
cout << -1 << "\n";
}
백준 BOJ 7827번 : Transitive Closure
문제 난이도 : Silver I
알고리즘 분류 : 그래프 탐색
그래프가 주어질 때 i != j인 (i, j)에 대해 i에서 j로 가는 경로의 수를 구하는 문제이다.
간단한 그래프 탐색으로 풀이할 수 있으며, 모든 노드에 대해 다른 모든 노드의 방문 여부를 탐색해주어야 한다.
주의할 점은 이 문제에서 주어지는 간선은 단방향 간선이며, 마지막에 방문 여부를 count 해줄 때 출발 노드는 카운트에서 제외해주어야 한다는 것이다.
다만 이 경우 예제를 넣어보면 실수했는지 바로 알 수 있기 때문에 틀릴 염려는 크게 없을 것이다.
#include <bits/stdc++.h>
#define int long long
using namespace std;
vector<vector<int>> adj;
vector<bool> vis;
void f(int x) {
vis[x] = true;
for(int i=0; i<adj[x].size(); i++) {
int y = adj[x][i];
if(!vis[y]) f(y);
}
}
main() {
ios_base::sync_with_stdio(false);
cin.tie(NULL), cout.tie(NULL);
int T; cin >> T;
while(T--) {
int N, M; cin >> N >> M;
adj.clear();
adj.resize(N+1);
while(M--) {
int a, b; cin >> a >> b;
adj[a].push_back(b);
}
int ans = 0;
for(int i=1; i<=N; i++) {
vis.clear();
vis.resize(N+1);
f(i);
for(int j=1; j<=N; j++) {
if(i == j) continue;
if(vis[j]) ans++;
}
}
cout << ans << "\n";
}
}
백준 BOJ 17241번 : Pineapple Advertising
문제 난이도 : Silver I
알고리즘 분류 : 그래프 탐색
그래프가 주어지고, K개의 쿼리에 대해 어떤 점을 선택했을 때 그 노드와 그 노드와 간선 하나로 연결된 모든 노드들 중 지금까지 선택되지 않은 노드들이 새로 선택된다고 할 때 새로 선택되는 노드의 개수를 쿼리마다 구하는 문제이다.
adj 벡터에 인접한 노드들을 저장해주고, 이들을 체크하면서 인접한 것들 중 체크되지 않은 것들을 count 하면서 세어주면 된다.
다만 그냥 제출할 경우 시간 초과가 발생하는데, 예를 들어 1번 노드에 10만 개의 노드가 연결되어있고 1번 노드에 대한 쿼리를 10만 번 수행하면 시간 초과가 발생한다.
따라서 한 번 언급되었던 노드는 다시 선택해도 새롭게 선택되는 노드의 수가 0이므로, 쿼리로 한 번 입력받은 노드 번호는 따로 저장해두었다가 다시 입력될 경우 0을 출력하면 시간 초과를 피할 수 있다.
#include <bits/stdc++.h>
#define int long long
using namespace std;
main() {
ios_base::sync_with_stdio(false);
cin.tie(NULL), cout.tie(NULL);
int N, M, K; cin >> N >> M >> K;
vector<vector<int>> adj(N+1);
while(M--) {
int a, b; cin >> a >> b;
adj[a].push_back(b);
adj[b].push_back(a);
}
vector<bool> v(N+1), u(N+1);
while(K--) {
int x; cin >> x;
int ans = 0;
if(u[x]) {
cout << ans << "\n";
continue;
}
u[x] = true;
if(!v[x]) {
ans++;
v[x] = true;
}
for(int i=0; i<adj[x].size(); i++) {
int y = adj[x][i];
if(!v[y]) {
ans++;
v[y] = true;
}
}
cout << ans << "\n";
}
}
백준 BOJ 15420번 : Paint bucket
문제 난이도 : Silver I
알고리즘 분류 : 그래프 탐색
N x M 크기의 배열이 주어지고 하나의 칸을 선택하여 문자를 바꾼다고 할 때, 원래 있던 문자와 상하좌우로 인접하여 같은 문자들도 모두 같은 문자로 바뀐다면 선택 이후 배열의 상태를 출력하는 문제이다.
그래프 탐색(DFS 또는 BFS)를 이용하여 상하좌우로 같은 값인 배열의 값들을 모두 바꾸어주면 되는 간단한 문제이다.
#include <bits/stdc++.h>
#define int long long
using namespace std;
int N, M;
char col;
vector<vector<char>> v;
vector<vector<bool>> vis;
void f(int x, int y, char c) {
vis[x][y] = true;
v[x][y] = col;
int dx[4] = {1, -1, 0, 0};
int dy[4] = {0, 0, 1, -1};
for(int i=0; i<4; i++) {
int nx = x + dx[i];
int ny = y + dy[i];
if(nx < 0 || ny < 0 || nx >= N || ny >= M) continue;
if(v[nx][ny] != c || vis[nx][ny]) continue;
f(nx, ny, c);
}
}
main() {
ios_base::sync_with_stdio(false);
cin.tie(NULL), cout.tie(NULL);
cin >> N >> M;
v.resize(N, vector<char>(M));
for(int i=0; i<N; i++)
for(int j=0; j<M; j++) cin >> v[i][j];
int bx, by; cin >> bx >> by >> col;
vis.resize(N, vector<bool>(M));
f(bx, by, v[bx][by]);
for(int i=0; i<N; i++) {
for(int j=0; j<M; j++) cout << v[i][j];
cout << "\n";
}
}
백준 BOJ 18419번 : 桁和 (Digit Sum)
문제 난이도 : Silver I
알고리즘 분류 : DP
어떤 수에 각 자리수의 합을 더해서 새로운 수를 만들 때, 어떤 수 N을 만들 수 있는 다른 수의 개수를 구하는 문제이다. (예를 들어 13이 있으면 13 + 1 + 3으로 17을 만들 수 있다.)
일단 각 수는 자기 자신 그대로가 하나의 상태이므로 최소 1가지의 답이 있다.
그리고 a에서 b를 만들고, b에서 c를 만들 수 있다면 a에서 c 또한 만들 수 있으므로 b에 a의 경우를 누적해서 더해주는 식으로 답을 구해주면 된다.
따라서 다음과 같이 dp를 활용하여 1부터 N까지 경우의 수를 세어 뒤로 누적해주면서 답을 구해주면 된다.
그래프 이론에도 태그 분류가 되어있는 문제라 BFS로 풀려고 했는데 dp 풀이가 더 간단한 것 같다.
#include <bits/stdc++.h>
#define int long long
using namespace std;
main() {
ios_base::sync_with_stdio(false);
cin.tie(NULL), cout.tie(NULL);
int N; cin >> N;
vector<int> dp(N+1, 1);
for(int i=1; i<=N; i++) {
int temp = i, sum = 0;
while(temp > 0) {
sum += temp % 10;
temp /= 10;
}
if(i + sum <= N) dp[i + sum] += dp[i];
}
cout << dp[N] << "\n";
}
백준 BOJ 21189번 : On Average They're Purple
문제 난이도 : Silver I
알고리즘 분류 : BFS
한 명이 주어진 그래프의 간선들을 빨간색 혹은 파란색으로 칠하고, 나머지 한 명은 그 그래프의 1번 노드에서 N번 노드까지 경로에서 중간에 간선의 색이 바뀌는 횟수를 최소화할 때, 그 횟수를 구하는 문제이다.
1번 노드에서 N번 노드로 가는데 필요한 최단 거리에 모두 빨간색과 파란색이 번갈아가며 나오게 하면 (최단 거리 - 1)만큼 색의 변경이 나타난다.
동시에 다른 경로에 대해서도 적절한 색의 배치를 통해 (최단 거리 - 1)회 이상의 색 변경이 나타나게 할 수 있다.
따라서 BFS로 1번 노드에서부터 N번 노드까지의 거리를 구하고 -1을 하여 답을 구해주면 된다.
#include <bits/stdc++.h>
#define int long long
using namespace std;
main() {
ios_base::sync_with_stdio(false);
cin.tie(NULL), cout.tie(NULL);
int N, M; cin >> N >> M;
vector<vector<int>> adj(N+1);
while(M--) {
int a, b; cin >> a >> b;
adj[a].push_back(b);
adj[b].push_back(a);
}
vector<int> dis(N+1, -1);
dis[1] = 0;
queue<int> q;
q.push(1);
while(!q.empty()) {
int x = q.front();
q.pop();
if(x == N) {
int ans = dis[N] - 1;
cout << ans << "\n";
break;
}
for(int i=0; i<adj[x].size(); i++) {
int y = adj[x][i];
if(dis[y] != -1) continue;
dis[y] = dis[x] + 1;
q.push(y);
}
}
}
백준 BOJ 2545번 : 팬케익 먹기
문제 난이도 : Bronze I
알고리즘 분류 : 구현
직육면체의 세 변의 길이가 주어지고 가로, 세로, 높이에서 합쳐서 1cm씩 N번 감소시켜서 만들 수 있는 최대 부피를 구하는 문제이다.
곱의 값은 각 수의 크기가 비슷할 수록 커지므로, 결국은 N을 3개로 분배하여 세 값이 최대한 비슷하게 하는 것이 목표이다.
따라서 나올 수 있는 경우를 모두 그려보면 다음과 같다.
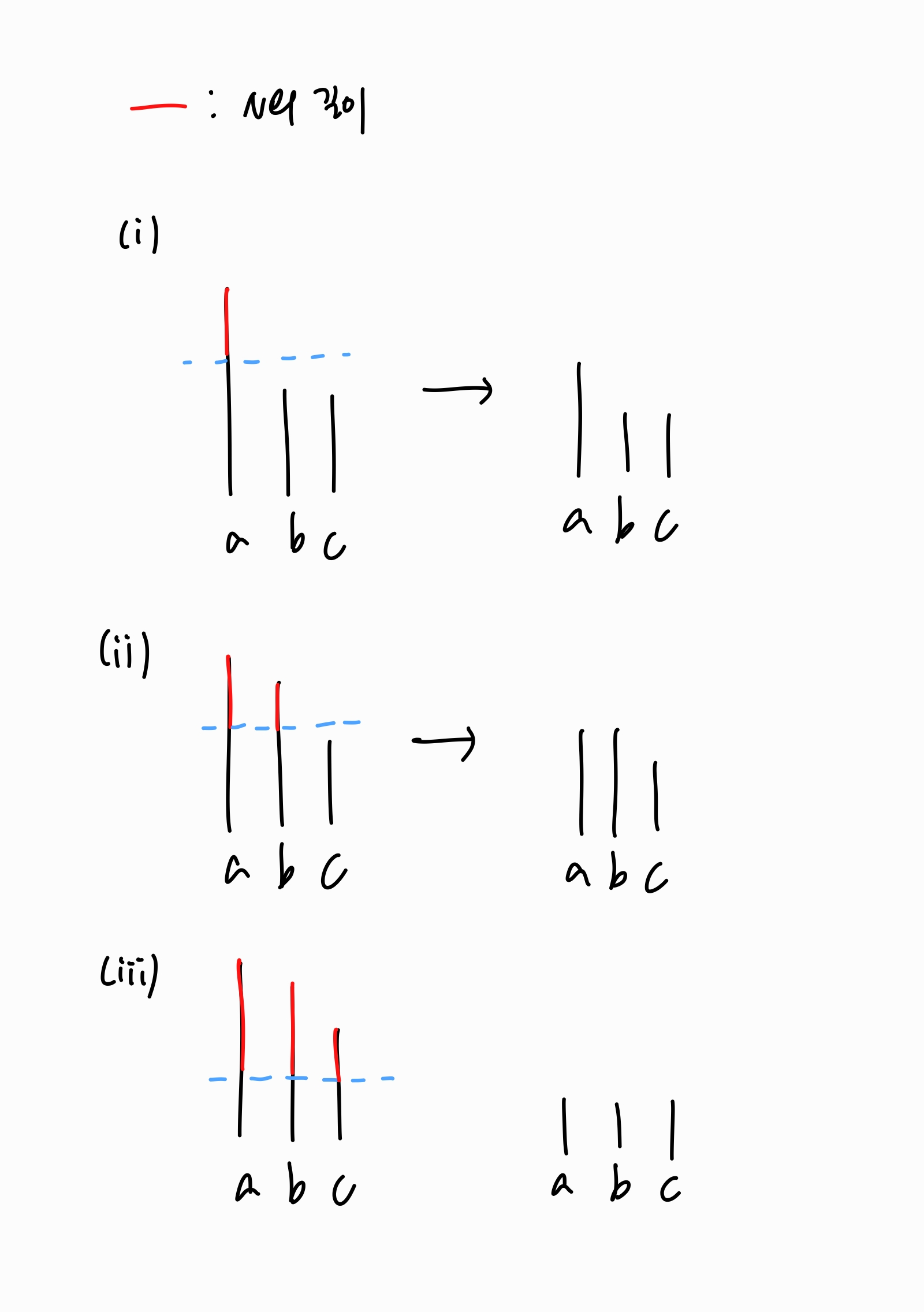
세 가지 경우에 따라 나눠서 N을 분배해서 a, b, c 값을 감소시켜주면 된다.
N은 항상 정수로만 분배해야 하므로 예를 들어 (ii)의 케이스에서 1이 남는다던지, (iii)의 케이스에서 1이나 2가 남을 수 있다.
이 경우는 나머지를 남겨서 따로 추가로 빼주는 등의 방식으로 답을 구해줄 수 있다.
자세한 처리는 코드를 참고하자.
#include <bits/stdc++.h>
#define int long long
using namespace std;
main() {
ios_base::sync_with_stdio(false);
cin.tie(NULL), cout.tie(NULL);
int T; cin >> T;
while(T--) {
vector<int> v(3);
for(int i=0; i<3; i++) cin >> v[i];
sort(v.begin(), v.end(), greater<int>());
int x; cin >> x;
if(v[0] - v[1] >= x) {
cout << (v[0] - x) * v[1] * v[2] << "\n";
continue;
}
x -= v[0] - v[1];
v[0] = v[1];
if((v[0] - v[2])*2 >= x) {
cout << (v[0] - x/2) * (v[1] - (x - x/2)) * v[2] << "\n";
continue;
}
x -= (v[0] - v[2]) * 2;
v[0] = v[2];
v[1] = v[2];
v[0] -= x/3;
v[1] -= x/3;
v[2] -= x/3;
if(x % 3 == 1) v[2]--;
else if(x % 3 == 2) v[1]--, v[2]--;
cout << v[0] * v[1] * v[2] << "\n";
}
}
백준 BOJ 8783번 : Architektura niezależna
문제 난이도 : Silver III
알고리즘 분류 : 그래프 탐색
N x N 배열에 '#' 문자로 둘러싸인 도형이 있을 때, 그 도형을 포함한 내부 공간의 면적을 구하는 문제이다.
구현을 통해 어떤 점이 공간의 내부 점인지를 파악하기는 가능은 하지만, 구현량이 꽤 많아진다.
따라서 배열의 가장자리에서부터의 탐색을 통해 건물 바깥의 점들을 모두 찾아주자.
그런 뒤 N x N의 값에서 건물 바깥 점들의 개수를 빼주면 답을 얻을 수 있다.
#include <bits/stdc++.h>
#define int long long
using namespace std;
int N, cnt;
vector<vector<char>> v;
vector<vector<bool>> vis;
void f(int x, int y) {
vis[x][y] = true;
cnt++;
int dx[4] = {1, -1, 0, 0};
int dy[4] = {0, 0, 1, -1};
for(int i=0; i<4; i++) {
int nx = x + dx[i];
int ny = y + dy[i];
if(nx < 0 || ny < 0 || nx >= N || ny >= N) continue;
if(v[nx][ny] != '.' || vis[nx][ny]) continue;
f(nx, ny);
}
}
main() {
ios_base::sync_with_stdio(false);
cin.tie(NULL), cout.tie(NULL);
int T; cin >> T;
while(T--) {
cin >> N;
v.clear();
v.resize(N, vector<char>(N));
for(int i=0; i<N; i++)
for(int j=0; j<N; j++) cin >> v[i][j];
vis.clear();
vis.resize(N, vector<bool>(N));
cnt = 0;
for(int i=0; i<N; i++)
for(int j=0; j<N; j++)
if(i == 0 || j == 0 || i == N-1 || j == N-1) {
if(v[i][j] == '.' && !vis[i][j]) f(i, j);
}
int ans = N*N - cnt;
cout << ans << "\n";
}
}
백준 BOJ 9700번 : RAINFOREST CANOPY
문제 난이도 : Silver II
알고리즘 분류 : 그래프 탐색
N x N 배열에 1과 0으로 이루어진 배열이 주어질 때, 상하좌우 및 대각선으로 이동하여 인접한 1을 같은 덩어리라고 할 때 1의 덩어리의 수를 구하는 문제이다.
간단한 그래프 탐색 문제로, BFS나 DFS와 같은 그래프 탐색 알고리즘을 통해 몇 개의 덩어리가 존재하는지 찾아주면 된다.
#include <bits/stdc++.h>
#define int long long
using namespace std;
int N;
vector<vector<char>> v;
vector<vector<bool>> vis;
void f(int x, int y) {
vis[x][y] = true;
int dx[8] = {-1, -1, -1, 0, 1, 1, 1, 0};
int dy[8] = {-1, 0, 1, 1, 1, 0, -1, -1};
for(int i=0; i<8; i++) {
int nx = x + dx[i];
int ny = y + dy[i];
if(nx < 0 || ny < 0 || nx >= N || ny >= N) continue;
if(v[nx][ny] != '1' || vis[nx][ny]) continue;
f(nx, ny);
}
}
main() {
ios_base::sync_with_stdio(false);
cin.tie(NULL), cout.tie(NULL);
int t = 1;
while(cin >> N) {
v.clear();
v.resize(N, vector<char>(N));
for(int i=0; i<N; i++)
for(int j=0; j<N; j++) cin >> v[i][j];
vis.clear();
vis.resize(N, vector<bool>(N));
int ans = 0;
for(int i=0; i<N; i++)
for(int j=0; j<N; j++)
if(v[i][j] == '1' && !vis[i][j]) {
f(i, j);
ans++;
}
cout << "Case #" << t << ": " << ans << "\n";
t++;
}
}
백준 BOJ 18126번 : 너구리 구구
문제 난이도 : Silver II
알고리즘 분류 : 그래프 탐색
노드가 N개이고 간선이 N-1개인 트리가 주어질 때, 1번 노드에서 가장 먼 노드까지의 거리를 구하는 문제이다.
이 역시 간단한 그래프 탐색 문제로, 1번 노드로부터 DFS나 BFS 등으로 모든 노드까지의 거리를 구하고 그 중 최댓값을 구해주면 된다.
나는 그냥 탐색 중에 DFS 함수에서 바로 갱신하도록 구현해주었다.
#include <bits/stdc++.h>
#define int long long
using namespace std;
vector<vector<pair<int, int>>> adj;
vector<int> dis;
int ans = 0;
void f(int x) {
ans = max(ans, dis[x]);
for(int i=0; i<adj[x].size(); i++) {
int y = adj[x][i].first;
if(dis[y] != -1) continue;
dis[y] = dis[x] + adj[x][i].second;
f(y);
}
}
main() {
ios_base::sync_with_stdio(false);
cin.tie(NULL), cout.tie(NULL);
int N; cin >> N;
adj.resize(N+1);
for(int i=0; i<N-1; i++) {
int a, b, c; cin >> a >> b >> c;
adj[a].push_back({b, c});
adj[b].push_back({a, c});
}
dis.resize(N+1, -1);
dis[1] = 0;
f(1);
cout << ans << "\n";
}
백준 BOJ 21325번 : Free food
문제 난이도 : Silver II
알고리즘 분류 : 그래프 탐색
N개의 노드의 부모 노드가 주어지고, 참석한 사람들의 노드가 주어질 때, 어떤 노드의 조상 노드 중에 참석한 사람이 없다면 그 사람이 돈을 내야한다고 할 때 돈을 내는 사람의 수를 구하는 문제이다.
즉, 거꾸로 생각해보면 루트 노드에서부터 내려오면서 만나는 노드가 있으면 카운트 해주고 그 밑으로는 검사를 안하면 된다.
따라서 노드를 반대로 연결하여 부모 노드가 자식 노드를 가리키게 연결한다.
그 다음 0번 노드(또는 루트 노드로 해도 된다. 어차피 0번 노드가 루트 노드의 부모이다.)에서부터 내려오면서 탐색하면서 목록에 해당 노드가 있으면 count 후 continue 해주고, 아니면 그 노드의 자식들을 검사해주면 된다.
N과 M이 모두 10만 이하이길래 혹시나 해서 M개의 노드 목록 중에서 검색할 때 이분 탐색으로 찾을 수 있도록 구현했다.
생각해보니까 이렇게 안하면 시간 초과가 발생할 것 같다.
#include <bits/stdc++.h>
#define int long long
using namespace std;
main() {
ios_base::sync_with_stdio(false);
cin.tie(NULL), cout.tie(NULL);
int N, M; cin >> N >> M;
vector<vector<int>> adj(N+1);
for(int i=1; i<=N; i++) {
int x; cin >> x;
adj[x].push_back(i);
}
vector<int> v(M);
for(int i=0; i<M; i++) cin >> v[i];
sort(v.begin(), v.end());
queue<int> q;
q.push(0);
int ans = 0;
while(!q.empty()) {
int x = q.front();
q.pop();
if(upper_bound(v.begin(), v.end(), x) - lower_bound(v.begin(), v.end(), x) > 0) {
ans++;
continue;
}
for(int i=0; i<adj[x].size(); i++) q.push(adj[x][i]);
}
cout << ans << "\n";
}
백준 BOJ 24164번 : 光ファイバー網の整備 (Fiber)
문제 난이도 : Silver I
알고리즘 분류 : 분리 집합
몇 개의 간선으로 연결된 그래프가 주어질 때, 이 그래프가 연결 그래프가 되기 위해서 추가해야 하는 간선의 수를 구하는 문제이다.
만약 그래프가 N개의 덩어리로 구성되어 있다면, N-1개의 간선을 연결하여 하나의 connected graph로 만들 수 있다.
따라서, 그래프가 몇 덩어리로 구성되어 있는지를 찾아주면 되고 이것은 분리 집합(union find)으로 쉽게 구현할 수 있다.
자세한 구현은 다음의 코드를 참조하자.
#include <bits/stdc++.h>
#define int long long
using namespace std;
vector<int> v;
int f(int x) {
if(x == v[x]) return x;
else return v[x] = f(v[x]);
}
main() {
ios_base::sync_with_stdio(false);
cin.tie(NULL), cout.tie(NULL);
int N, M; cin >> N >> M;
v.resize(N+1);
for(int i=1; i<=N; i++) v[i] = i;
while(M--) {
int a, b; cin >> a >> b;
if(f(a) != f(b)) v[f(a)] = f(b);
}
vector<int> u(N);
for(int i=0; i<N; i++) u[i] = f(i+1);
sort(u.begin(), u.end());
u.erase(unique(u.begin(), u.end()), u.end());
int ans = u.size() - 1;
cout << ans << "\n";
}
백준 BOJ 21425번 : Лабиринт
문제 난이도 : Silver I
알고리즘 분류 : BFS
3차원 지도에서 '1'의 위치에서 '2'의 위치로 '.'을 따라서 이동하는 최단 거리 * 5의 값을 구하는 문제이다.
3차원 BFS를 구현하여 풀이해주면 된다.
이 때 아래층으로는 내려갈 수 있지만 위층으로는 갈 수 없으므로, 단위 벡터로 만들어 줄 수 있는 방향은 상하좌우 + 아래로 5가지가 있다.
모든 칸에서마다 이 5가지에 대해 BFS 탐색을 수행해주면 된다.
또한 한 칸을 이동하는데 5초가 걸린다고 하였으므로 답에 5를 곱해주는 것을 잊지말자.
#include <bits/stdc++.h>
#define int long long
using namespace std;
struct s { int x, y, z; };
main() {
ios_base::sync_with_stdio(false);
cin.tie(NULL), cout.tie(NULL);
int N, M, K; cin >> N >> M >> K;
vector<vector<vector<int>>> dis(N, vector<vector<int>>(M, vector<int>(K, -1)));
queue<s> q;
vector<vector<vector<char>>> v(N, vector<vector<char>>(M, vector<char>(K)));
for(int i=0; i<N; i++)
for(int j=0; j<M; j++)
for(int k=0; k<K; k++) {
cin >> v[i][j][k];
if(v[i][j][k] == '1') {
dis[i][j][k] = 0;
q.push({i, j, k});
}
}
while(!q.empty()) {
int x = q.front().x;
int y = q.front().y;
int z = q.front().z;
q.pop();
if(v[x][y][z] == '2') {
cout << dis[x][y][z] * 5 << "\n";
break;
}
int dx[5] = {1, 0, 0, 0, 0};
int dy[5] = {0, 1, -1, 0, 0};
int dz[5] = {0, 0, 0, 1, -1};
for(int i=0; i<5; i++) {
int nx = x + dx[i];
int ny = y + dy[i];
int nz = z + dz[i];
if(nx >= N || ny < 0 || nz < 0 || ny >= M || nz >= K) continue;
if(v[nx][ny][nz] == 'o' || dis[nx][ny][nz] != -1) continue;
dis[nx][ny][nz] = dis[x][y][z] + 1;
q.push({nx, ny, nz});
}
}
}
백준 BOJ 24819번 : Escape Wall Maria
문제 난이도 : Silver I
알고리즘 분류 : BFS
'S' 지점에서 시작하여 주어진 배열의 가장 외곽으로 나가는 최단 거리를 구하는 문제이다.
다만 이 때 U, D, L, R이라고 써 있는 칸은 해당 방향에서만 들어올 수 있으며, 주어진 제한 시간 안에 나가지 못할 경우 NOT POSSIBLE을 출력해야 한다.
BFS로 구현하되, 위에서 언급된 조건대로 구현하기 위해 몇 가지 코드를 더 작성해야 한다.
dx dy값과 배열의 값을 비교하여 올바른 방향이 아닌 경우 continue로 넘겨준다.
또한 마지막에 제한 시간 안에 들어올 수 있는지도 검사를 해주어야 한다.
#include <bits/stdc++.h>
#define int long long
using namespace std;
main() {
ios_base::sync_with_stdio(false);
cin.tie(NULL), cout.tie(NULL);
int K, N, M; cin >> K >> N >> M;
vector<vector<int>> dis(N, vector<int>(M, -1));
queue<pair<int, int>> q;
vector<vector<char>> v(N, vector<char>(M));
for(int i=0; i<N; i++)
for(int j=0; j<M; j++) {
cin >> v[i][j];
if(v[i][j] == 'S') {
dis[i][j] = 0;
q.push({i, j});
}
}
while(!q.empty()) {
int x = q.front().first;
int y = q.front().second;
q.pop();
if(x == 0 || x == N-1 || y == 0 || y == M-1) {
if(dis[x][y] <= K) cout << dis[x][y] << "\n";
else cout << "NOT POSSIBLE\n";
return 0;
}
int dx[4] = {1, -1, 0, 0};
int dy[4] = {0, 0, 1, -1};
for(int i=0; i<4; i++) {
int nx = x + dx[i];
int ny = y + dy[i];
if(nx < 0 || ny < 0 || nx >= N || ny >= M) continue;
if(v[nx][ny] == '1' || dis[nx][ny] != -1) continue;
if(i != 0 && v[nx][ny] == 'U') continue;
if(i != 1 && v[nx][ny] == 'D') continue;
if(i != 2 && v[nx][ny] == 'L') continue;
if(i != 3 && v[nx][ny] == 'R') continue;
dis[nx][ny] = dis[x][y] + 1;
q.push({nx, ny});
}
}
cout << "NOT POSSIBLE\n";
}
'알고리즘 > 알고리즘 공부 내용 정리' 카테고리의 다른 글
| 백준 BOJ 풀이 : 플로이드-워셜 알고리즘 문제들 풀이 220730 (0) | 2022.07.30 |
|---|---|
| 백준 BOJ 풀이 : 그래프 이론 문제들 (Silver I ~ Gold) 220729 (0) | 2022.07.29 |
| 백준 BOJ 풀이 : 각종 Silver 난이도 그래프 문제들 220727 (0) | 2022.07.27 |
| 백준 BOJ 풀이 : 오늘도 그래프 탐색 문제 220726 (0) | 2022.07.26 |
| 백준 BOJ 풀이 : BFS 문제들 위주 풀이 (그래프 탐색) 220725 (0) | 2022.07.25 |