백준 BOJ 13279번 : 곱의 합 쿼리
문제 난이도 : Platinum IV (FFT로 해결할 시 체감 난이도 Platinum I, 그러나 O(N^2) 풀이가 통과되어 하향 조정)
알고리즘 분류 : FFT (고속 푸리에 변환)

N개의 수로 이루어진 수열 A에서, 쿼리 K가 주어지면 A의 길이 K인 부분 수열들의 곱의 합을 구하여 출력하는 문제입니다.
이 때 쿼리 문제이므로 쿼리의 수는 최대 N개가 주어질 수 있습니다.

예를 들어 N = 3이고 A = { 1, 2, 3 }이라면, K = 2가 주어졌을 때 길이가 2인 부분 수열은 { 1, 2 }, { 1, 3 }, { 2, 3 }이 있으므로 이들의 곱의 합을 구하면 11이 됩니다.
문제 조건을 보면 쿼리는 최대 N개 들어올 수 있고 이는 결국 1 ~ N의 모든 수가 들어올 수 있다는 뜻이므로 모든 값들을 미리 계산하는 방법을 찾아야 합니다.

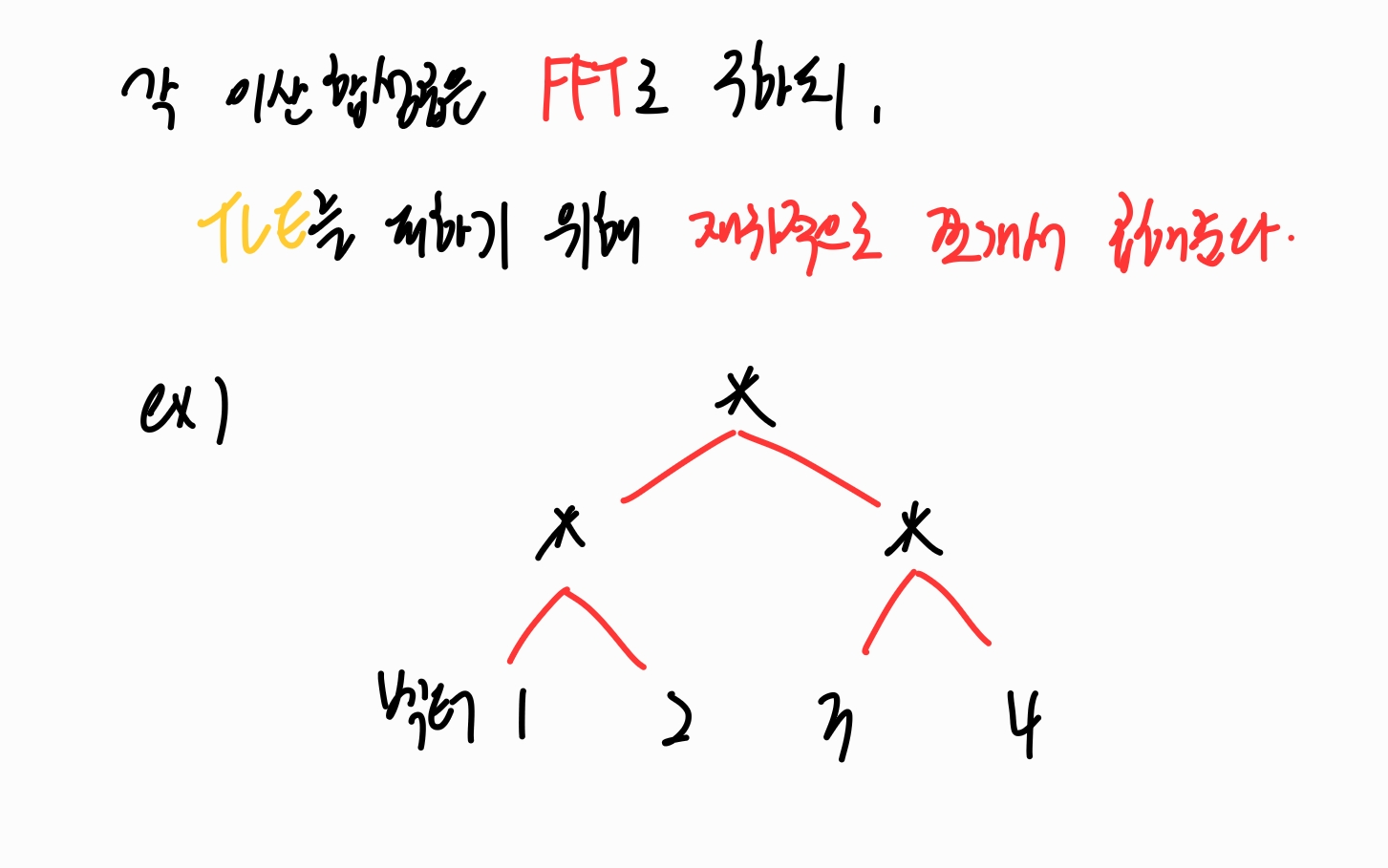
(맨 아랫줄에 더하기가 아니라 콤마가 들어가야 하는데 잘못 적었습니다.)
핵심 아이디어는, 항의 x 값과 다른 항의 1이 곱해지면 x가 된다는 점을 활용하여 (a_1, 1) * (a_2, 1) * ... * (a_N, 1)꼴의 식을 만들어주면 (여기서 각 항은 벡터를 의미하며 * 기호는 이산 합성곱을 의미합니다.) 최종적으로 구해지는 벡터의 각 항이 순서대로 쿼리가 요구하는 값임을 알 수 있습니다.
따라서 위의 식을 계산하면 됨을 알 수 있습니다.
그렇다면 이 식을 어떻게 계산할 수 있을까요?
이산 합성 곱들의 반복이므로 우선 FFT를 생각해볼 수 있습니다.
그런데 벡터의 수가 N개나 되므로, 순서대로 곱하면 TLE가 발생할 것입니다.
따라서 이를 피하기 위해 재귀적으로 두 부분씩 쪼개서 곱해주는 Divide and Conquer 방식을 사용해줍니다.
#include <bits/stdc++.h>
#define int long long
using namespace std;
const double PI = acos(-1);
typedef complex<double> cpx;
const int MOD = (int)(1e5 + 3);
void FFT(vector<cpx> &v, bool inv) {
int S = v.size();
for(int i=1, j=0; i<S; i++) {
int bit = S/2;
while(j >= bit) {
j -= bit;
bit /= 2;
}
j += bit;
if(i < j) swap(v[i], v[j]);
}
for(int k=1; k<S; k*=2) {
double angle = (inv ? PI/k : -PI/k);
for(int i=0; i<S; i+=k*2) {
for(int j=0; j<k; j++) {
cpx even = v[i+j], odd = v[i+j+k];
cpx w = cpx(cos(angle*j), sin(angle*j));
v[i+j] = even + w*odd;
v[i+j+k] = even - w*odd;
}
}
}
if(inv)
for(int i=0; i<S; i++) v[i] /= S;
}
vector<cpx> mul(vector<cpx> v, vector<cpx> u) {
int S = 2;
while(S < v.size() + u.size()) S *= 2;
v.resize(S); FFT(v, false);
u.resize(S); FFT(u, false);
vector<cpx> w(S);
for(int i=0; i<S; i++) w[i] = v[i] * u[i];
FFT(w, true);
for(int i=0; i<S; i++) w[i] = {(int)round(w[i].real()) % MOD, 0};
return w;
}
vector<cpx> mul(const vector<vector<cpx>> &v, int l, int r) {
if(l == r) return v[l];
return mul(mul(v, l, (l+r)/2), mul(v, (l+r)/2 + 1, r));
}
main() {
ios_base::sync_with_stdio(false);
cin.tie(NULL), cout.tie(NULL);
int N; cin >> N;
vector<vector<cpx>> v(N);
for(int i=0; i<N; i++) {
int x; cin >> x;
v[i] = {cpx(x, 0), cpx(1, 0)};
}
vector<cpx> ans = mul(v, 0, N-1);
int M; cin >> M;
int MOD = (int)(1e6 + 3);
while(M--) {
int x; cin >> x;
cout << ans[N - x].real() << "\n";
}
}
풀이 코드는 위와 같습니다.
2차원 벡터를 선언하고, 각 벡터에 { a_i, 1 }을 저장해줍니다. (물론 각 원소는 cpx(a_i, 0), cpx(1, 0)과 같이 저장해줍니다.)
입력이 끝나면 이러한 벡터를 가지는 N개의 벡터가 존재합니다.
이제 이들을 재귀적으로 FFT를 수행해주기만 하면 됩니다.
재귀적으로 두 부분으로 쪼개서 곱하는 부분을 구현하는데 어려움이 있었는데, 함수를 오버로딩하여 해결하는 방법이 있어서 이를 참고하였습니다.

'알고리즘 > 백준(BOJ) 문제풀이' 카테고리의 다른 글
| 백준 BOJ 13055번 : K-Inversions 풀이 (FFT, 고속 푸리에 변환) (0) | 2022.06.29 |
|---|---|
| 백준 BOJ 13575번 : 보석 가게 풀이 (FFT, 고속 푸리에 변환) (0) | 2022.06.29 |
| 백준 BOJ 20176번 : Needle 풀이 (FFT, 고속 푸리에 변환) (0) | 2022.06.27 |
| BOJ 1067 이동, BOJ 22289 큰 수 곱셈 (3) (FFT, 고속 푸리에 변환) (0) | 2022.06.27 |
| 백준 BOJ 2934번 : LRH 식물 (느리게 갱신되는 세그먼트 트리) (0) | 2022.06.25 |