이 포스트에서는 프로그래밍 문제 사이트 백준 Online Judge BOJ 17318 Highway Cycling 문제의 풀이 코드와 해설을 다루고 있습니다.
문제 난이도는 Solved.ac 기준 Diamond I이며, 문제를 풀이하기 위해 라그랑주 승수법(Lagrange Multiplier Method)에 대한 배경지식과 이분탐색의 활용에 대한 이해가 필요합니다.
BOJ 17318 Highway Cycling
17318번: Highway Cycling
DanDan is always interested in challenging himself. This summer, he prepares to cycle along the Sichuan-Tibet highway to reach Lhasa. It is widely known that the Sichuan-Tibet Highway is filled with hauntingly beautiful scenery, but also happens to contain
www.acmicpc.net
↑ 문제 링크는 여기에 있습니다.

문제가 길지만 이를 짧게 요약하면 위와 같이 축약하여 정리할 수 있습니다.
주어진 구간의 수, 총 초기 에너지, 구간 거리, 저항 계수, 바람 속도가 주어지고 총 에너지를 모두 소모하여 구간별 속도를 최고가 되도록 하여야 최소 시간에 모든 구간을 통과할 수 있습니다.
즉, 우리는 구간별 속도 v_i를 결정해주기만 하면 계산을 통해 답을 도출할 수 있습니다.
그럼 이제 풀이를 작성해보겠습니다.

각 구간을 통과하는 시간은 s_i / v_i로 나타낼 수 있으므로, 우리는 그 시그마값을 구하면 됩니다.
s_i / v_i를 구하기 위해서는 에너지 식으로부터 v_i 값을 구해주어야 합니다.
따라서 우리는 T를 최소로 만드는 v_1 ~ v_N을 결정해주면 됩니다.
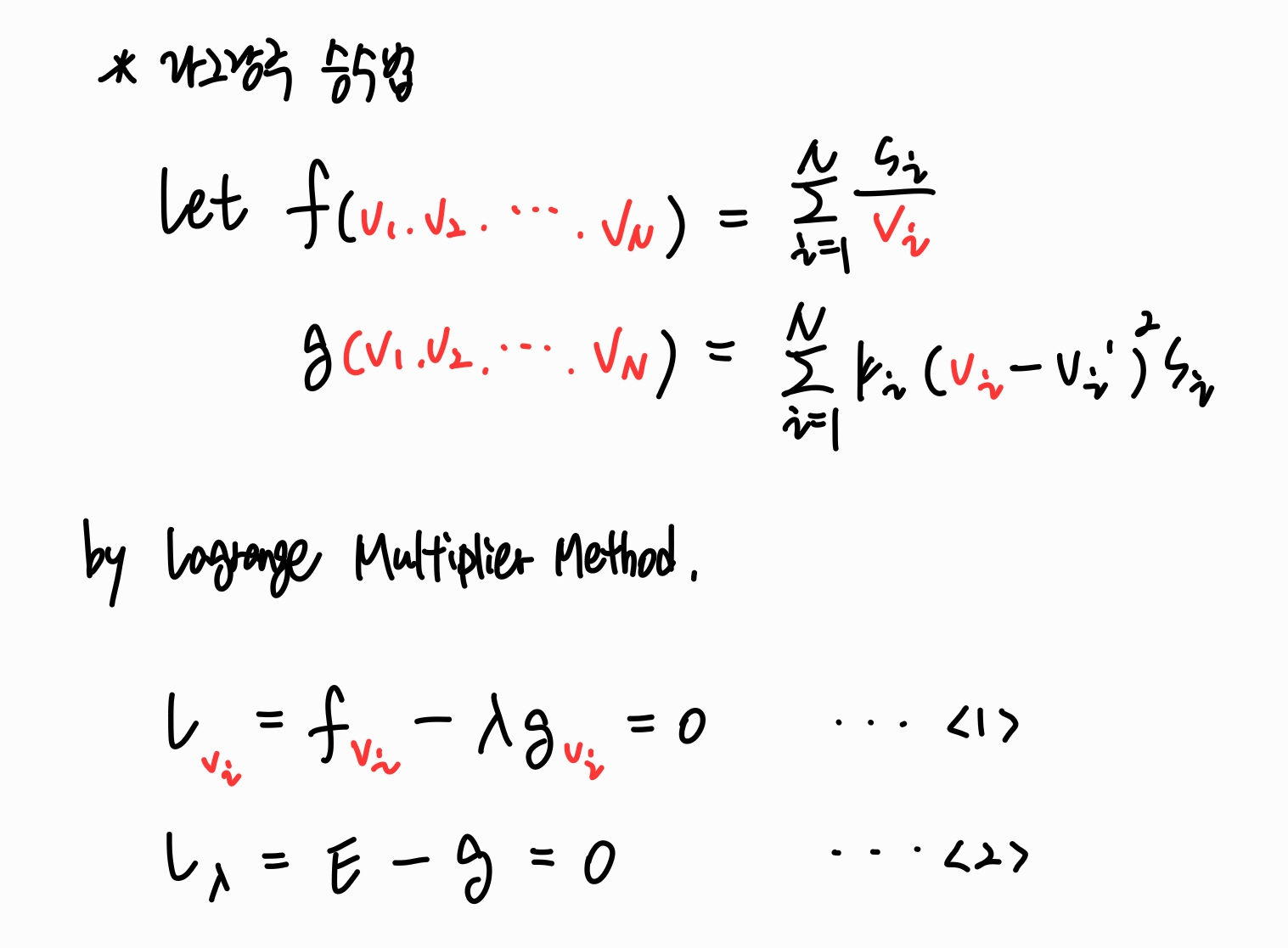
어떤 다변수 관계식을 가지고 다른 다변수 수식의 극값을 구하기 위해서 사용할 수 있는 것이 라그랑주 승수법(Lagrange Multiplier Method)입니다.
라그랑주 승수법에 대해 자세히 알고 싶다면 위키를 통해 내용을 참고하는 것을 추천드립니다.
여기서는 자세한 설명은 생략하고, 문제 상황을 라그랑주 승수법에 적용하여 풀이하는 과정만 정리하겠습니다.
+ 기호에 대한 설명을 추가하자면, L_(v_i)는 식을 v_i에 대해 미분했다는 뜻입니다.
f(v_1, v_2, ... , v_N)과 g(v_1, v_2, ... , v_N)을 위와 같이 잡으면, 라그랑주 승수법에 의해 위와 같이 "극값을 가지는 조건"으로 식 <1>과 식 <2>를 얻을 수 있습니다.
식 <1>은 모든 i에 대해 성립하는 식이므로 사실 N개의 식이지만, 모든 식이 같은 형태를 가지므로 서로 다른 i에 대한 식들로는 의미있는 계산을 이끌어낼 수 없습니다.
따라서 일반적인 i에 대한 식을 가지고 다루어보겠습니다.

식 <1>을 계산해보면 위와 같은 방정식이 얻어지게 됩니다.
기호가 많아보이지만 사실 변수는 v_i와 λ 두 개뿐입니다.
식을 한 쪽으로 넘겨 정리 후 생각해보면, E에 대한 식에서 v_i는 v_i'에 대한 델타값으로 양수 또는 음수를 가질 수 있습니다.
그러나 이 두 경우 중에서는 최소 T를 가지기 위해서 v_i > v_i'이어야 합니다.
따라서 식 <1>에서 얻어진 방정식에서, v_i - v_i' > 0이라고 둘 수 있습니다.
나머지 값들에 대한 부호도 적어보면, 모두 양수이므로 λ < 0이라는 것을 알 수 있습니다.
그러면 주어진 3차식에 대한 부호를 모두 결정했으므로 위와 같이 v_i에 대한 식 값 그래프의 개형을 그려볼 수 있습니다.
v_i > v_i'이라고 하였으므로, v_i는 위의 그래프에서 v_i'보다 오른쪽에서 값을 이분탐색해줄 수 있습니다.
v_i > v_i' 구간에서는 f '값이 변화하지 않으므로 단순 이분탐색으로 값을 찾아줄 수 있음을 확인할 수 있습니다.

구간을 확인했으므로 이제 연립을 통해 값을 구해볼 수 있습니다.
우리는 λ를 먼저 가정하고, 그 다음 나머지 변수들을 구해야하는데 3차 방정식이라서
따라서 여기서 이분탐색을 활용하여, v_i > v_i' 구간에서 v_i를 찾아주는 방법을 사용합니다. (여기서 v_i란 v_1 ~ v_N을 모두 찾아줌을 의미함)
그 다음 결정된 각 v_i를 식 <2>에 대입하여 E보다 크냐 작냐에 따라 ①에서 결정한 람다 값을 조정해줍니다.
이를 반복하여 람다가 결정이 되면, 이에 따라 v_i 값도 결정이 된 것이므로 이 v_i값을 우리가 구하고자 했던 f 값에 대입하여 답을 구해주면 됩니다.
→ 즉, 풀이 코드는 람다에 대한 이분탐색 내에서 N개의 변수에 대해 각각 이분탐색을 하는 복잡한 구조를 가지고 있습니다.
이제 위의 설명을 풀이 코드로 작성해보겠습니다.
#include <bits/stdc++.h>
using namespace std;
int main() {
ios_base::sync_with_stdio(false);
cin.tie(NULL), cout.tie(NULL);
cout << fixed;
cout.precision(8);
int N; cin >> N;
double E; cin >> E;
vector<double> s(N), k(N), v(N), v_(N);
for(int i=0; i<N; i++)
cin >> s[i] >> k[i] >> v_[i];
double l_left = -1e10, l_right = 0, l_mid;
for(int cnt=0; cnt<100; cnt++) {
l_mid = (l_left + l_right)/2;
double sum = 0;
for(int i=0; i<N; i++) {
double v_left = v_[i], v_right = 1e8, v_mid;
for(int cnt2=0; cnt2<100; cnt2++) {
v_mid = (v_left + v_right)/2;
double temp = 2*l_mid*k[i]*v_mid*v_mid*(v_mid-v_[i]) + 1;
if(temp < 0) v_right = v_mid;
else if(temp > 0) v_left = v_mid;
}
v[i] = v_mid;
sum += k[i]*(v[i]-v_[i])*(v[i]-v_[i])*s[i];
}
if(sum < E) l_left = l_mid;
else if(sum > E) l_right = l_mid;
}
double ans = 0;
for(int i=0; i<N; i++) ans += s[i]/v[i];
cout << ans;
}
코드 자체는 위에서 한 설명을 그대로 식 계산에만 대입한 것이므로 크게 설명할 부분은 없습니다.
10^(-6) 범위 내로 오차를 줄여야하기 때문에 cout에서 precision을 조절해주고, 이분탐색 구간에서 cnt 횟수를 늘려주면 정확도가 올라갑니다.

제출해보면 위와 같이 정답 처리를 받을 수 있습니다.
+ 이분탐색을 수행하는 cnt 수를 줄이면 풀이 시간이 감소할 것이라고 생각합니다.
'알고리즘 > 백준(BOJ) 문제풀이' 카테고리의 다른 글
| 백준 BOJ 최단 경로 알고리즘 3가지 활용 예시 (다익스트라, 벨만-포드, 플로이드-와셜) (0) | 2022.03.30 |
|---|---|
| 백준 BOJ 13174 괄호 풀이 (카탈란 삼각형, Diamond IV) (0) | 2022.03.29 |
| C++ getline EOF 조건문 없이 종료시키는 방법 (BOJ 10820) (0) | 2022.03.21 |
| [백준/BOJ] 3474번 : 교수가 된 현우, 22864번 : 피로도, 13458번 : 시험 감독 (0) | 2022.03.21 |
| C++ 해시맵 활용 : 리스트에 문자열이 있는지 검사하기 (BOJ 14425) (0) | 2022.03.20 |