이 포스트에서는 프로그래밍 문제 사이트 백준 Online Judge(BOJ)의 11444번 : '피보나치 수 6' 문제의 풀이 코드와 해설을 다루고 있습니다.
문제 난이도는 Solved.ac 기준 Gold IV에 해당하며, 문제를 풀이하기 위해 분할정복을 이용한 거듭제곱과 행렬 식 조작에 대한 이해가 필요합니다.
11444번 : 피보나치 수 6
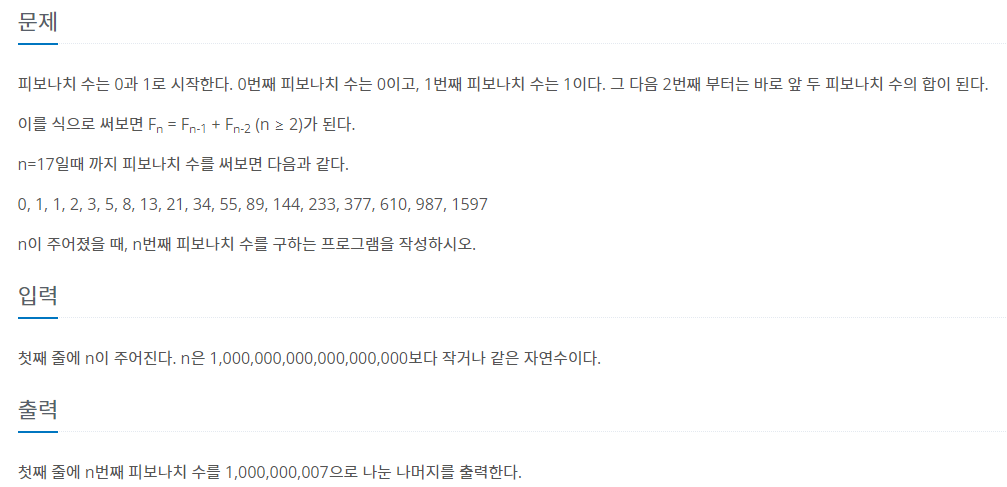
N번째 피보나치 수를 구하되, N이 엄청나게 큰 경우 이를 구하는 문제입니다.
O(N) 시간에는 해결이 불가능한 범위로 N을 주었으므로, O(log N) 시간 즉 빠른 거듭제곱을 반드시 활용해야 하는 문제입니다.
깔끔한 풀이를 위해 다른 분들의 풀이를 조금 읽어봤는데 유도 과정을 자세히 정리한 사람은 없는 것 같아 다음과 같이 따로 정리하여 첨부합니다.

점화식이 주어진 문제를 거듭제곱으로 풀이하기 위해서는 행렬식을 활용하여 식을 만들어주어야 합니다.
점화식에서 거듭제곱이 되는 행렬은 [ [1, 1], [1, 0] ]인데 식을 더욱 단순하게 만들어주기 위해 [ [F_2, F_1], [F_1, F_0] ]을 배치하여 식을 합쳐주면 됩니다.
참고로 초기 행렬 상태는 n = 0일 때 이므로 [ [1, 0], [0, 1] ]로 두면 됩니다.
이제 위의 식을 코드로 구현해주기만 하면 되며, 행렬의 거듭제곱 과정에서 빠른 거듭제곱으로만 수행이 되게끔 만들어주면 됩니다.
#include <bits/stdc++.h>
#define MOD 1000000007
using namespace std;
typedef vector<vector<long long>> matrix;
matrix multiply(matrix& A, matrix& B) {
matrix C = {{0, 0}, {0, 0}};
for(int i=0; i<2; i++)
for(int j=0; j<2; j++)
for(int k=0; k<2; k++)
C[i][j] = (C[i][j] + A[i][k]*B[k][j]) % MOD;
return C;
}
int main() {
ios_base::sync_with_stdio(false);
cin.tie(NULL), cout.tie(NULL);
long long N; cin >> N;
matrix ans = {{1, 0}, {0, 1}}, A = {{1, 1}, {1, 0}};
while(N > 0) {
if(N % 2 == 1)
ans = multiply(ans, A);
A = multiply(A, A);
N /= 2;
}
cout << ans[0][1];
}
행렬을 인자로 전달해주어야 하기 때문에 간단하게 구현하고자 배열을 사용하지 않고 vector를 활용하여 문제를 해결하였습니다.
행렬의 거듭제곱 과정에서 예를 들어 N = 9라고 하면 9는 이진수로 나타내면 1001이므로 ans = A * ((A^2)^2)^2임을 활용하여 ans에 A를 곱해놓고, A를 3번 거듭제곱 한 뒤 ans에 곱해주는 식으로 log N 시간에 구할 수 있도록 구현하였습니다.


이렇게 해서 백준 Online Judge(BOJ)의 단계별로 풀어보기에서 '분할 정복'까지 모든 문제를 풀이하였습니다.
다음 포스트에서는 '이분 탐색' 문제들 중에서 아직 풀지 않은 것들을 풀이해보도록 하겠습니다.
'알고리즘 > 백준(BOJ) 문제풀이' 카테고리의 다른 글
| [백준/BOJ] 2110번 : 공유기 설치, 1300번 : K번째 수 (이분 탐색) (0) | 2022.03.05 |
|---|---|
| [백준/BOJ] 10816번 : 숫자 카드 2, 1654번 : 랜선 자르기, 2805번 : 나무 자르기 (이분 탐색) (0) | 2022.03.05 |
| [백준/BOJ] 11401번 : 이항 계수 3, 10830번 : 행렬 제곱 (분할 정복, 빠른 거듭제곱) (0) | 2022.03.05 |
| [백준/BOJ] 1992번 : 쿼드트리, 1780번 : 종이의 개수, 1629번 : 곱셈 (분할 정복) (0) | 2022.03.04 |
| [백준/BOJ] 18258번 : 큐 2, 1021번 : 회전하는 큐, 5430번 : AC (큐, 덱) (0) | 2022.03.03 |