이 포스트는 프로그래밍 문제 사이트 백준 Online Judge(BOJ)의 16726번 : '영과일 학회방' 문제의 풀이 코드와 해설을 다루고 있습니다.
문제 난이도는 Solved.ac 기준 Platinum III에 해당하며, 문제를 풀이하기 위해 이분 매칭 알고리즘에 대한 이해가 필요합니다.
16726번 : 영과일 학회방
16726번: 영과일 학회방
영과일은 학회방이 없어질 위기에 처했지만 우수한 학회원들의 실력을 인정받아 학회방을 다시 배정 받을 수 있었다! 이에 행복해진 영과일 총무부장 재현이는 새로운 마음으로 1 × 2, 1 × 1 타
www.acmicpc.net
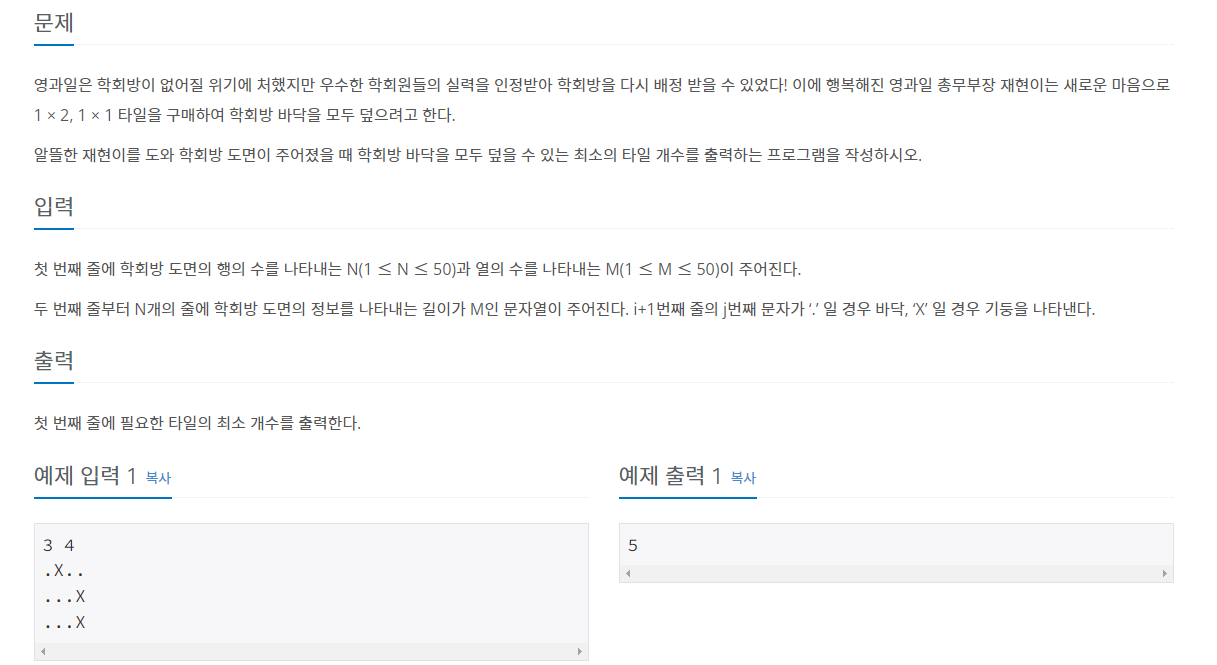
이전에 네트워크 플로우로 풀이를 시도하다가 이분 매칭에 더 특화된 문제라는 것을 알고 보류했었던 문제입니다.
X 표시된 칸을 피해서 '.'칸들을 2x1 타일 또는 1x1 타일들로 채울 때, 필요한 최소 타일의 수를 구하는 문제입니다.
당연하겠지만 2x1 타일을 최대한 사용하는 방법이 최소 타일을 사용하는 방법입니다.

이 문제를 푸는데 중요한 핵심 아이디어는, 주어진 map을 체스판의 검은 칸과 흰 칸처럼 나누어 생각했을 때, i+j가 홀수인 칸에서는 반드시 i+j가 짝수인 칸으로만 인접하여 이동할 수 있다는 것입니다. (반대도 마찬가지)
이를 활용하면 칸들을 두 그룹으로 나누어 생각할 수 있게 되고, 이는 곧 이분 매칭으로 문제를 해결할 수 있음을 의미합니다.
위의 예시는 3x3 판은 노드를 2개씩 넘버링 후 인접한 칸들에 대응되는 노드들을 간선으로 연결하고, 파란색으로 칠한 간선대로 2x1 타일을 채운 것입니다.
그리고 답을 간단하게 낼 수 있는데, 2x1 타일 하나는 빈 칸 2개를 차지하므로, 빈 칸의 수에서 최대 2x1 타일 수를 빼면 결국 최소 (2x1, 1x1) 타일 수가 됩니다.
↓ 풀이 코드는 아래의 접은 글에 정리되어 있습니다.
#include <bits/stdc++.h>
using namespace std;
const int MSIZE = 55, MAX = 1255;
vector<int> Adj[MAX];
int Left[MAX], Right[MAX];
bool Visit[MAX];
bool DFS(int from) {
Visit[from] = true;
for(int i=0; i<Adj[from].size(); i++) {
int to = Adj[from][i];
if(Right[to] == -1 || (!Visit[Right[to]] && DFS(Right[to]))) {
Left[from] = to, Right[to] = from;
return true;
}
}
return false;
}
int main() {
ios_base::sync_with_stdio(false);
cin.tie(NULL), cout.tie(NULL);
int N, M, block = 0; cin >> N >> M;
char Map[MSIZE][MSIZE];
for(int i=1; i<=N; i++) {
cin.clear();
for(int j=1; j<=M; j++) {
cin >> Map[i][j];
if(Map[i][j] == '.') block++;
}
}
int dir[2][4] = {{0, 0, -1, 1}, {-1, 1, 0, 0}};
for(int i=1; i<=N; i++)
for(int j=!(i%2)+1; j<=M; j+=2) {
if(Map[i][j] == 'X') continue;
for(int k=0; k<4; k++) {
int iNext = i+dir[0][k], jNext = j+dir[1][k];
if(iNext >= 1 && iNext <= N && jNext >= 1 && jNext <= M && Map[iNext][jNext] == '.')
Adj[((i-1)*50+j+1)/2].push_back(((iNext-1)*50+jNext+1)/2);
}
}
int match = 0;
fill(Left, Left+MAX, -1), fill(Right, Right+MAX, -1);
for(int i=1; i<MAX; i++) {
if(Left[i] == -1) {
fill(Visit, Visit+MAX, false);
if(DFS(i)) match++;
}
}
cout << block - match;
}
위의 모식도와 아이디어를 코드로 구현한 것입니다.
특히 넘버링 부분이 헷갈릴 수 있는데, 1행은 1번부터 시작하도록 구현하였기 때문에 1을 더해주고 2로 나눠주어야 합니다. (즉 2로 나누기 전에 2, 3, 4, 5, ...로 매겨야 함)
넘버링은 각자 짜는 방식이 다를 수 있으므로 이 부분은 편한대로 구현하시면 됩니다.
위의 풀이대로 코드를 작성하여 제출하면 위와 같은 기록으로 정답 처리를 받을 수 있습니다.
'알고리즘 > 백준(BOJ) 문제풀이' 카테고리의 다른 글
| [백준/BOJ] 13334번 : 철로 (스위핑 알고리즘, Gold II) (0) | 2022.02.19 |
|---|---|
| [백준/BOJ] 2533번 : 사회망 서비스(SNS) (DP) (0) | 2022.02.15 |
| [백준/BOJ] 3295번 : 단방향 링크 네트워크 (이분 매칭, Platinum II) (0) | 2022.01.19 |
| [백준/BOJ] 11014번 : 컨닝 2 (+ 1014번 : 컨닝) (이분매칭, Platinum II) (0) | 2022.01.19 |
| [백준/BOJ] 12843번 : 복수전공 (이분 매칭, Platinum III) (0) | 2022.01.19 |