이 포스트는 프로그래밍 문제 사이트 백준 Online Judge(BOJ)의 3938번 : 'Concert Hall Scheduling' 문제의 풀이 코드와 해설을 다루고 있습니다.
문제 난이도는 Solved.ac 기준 Platinum II에 해당하며, 문제를 풀이하기 위해 최소 비용 최대 유량(MCMF) 알고리즘에 대한 이해가 필요합니다.
3938번 : Concert Hall Scheduling
3938번: Concert Hall Scheduling
You are appointed director of a famous concert hall, to save it from bankruptcy. The hall is very popular, and receives many requests to use its two fine rooms, but unfortunately the previous director was not very efficient, and it has been losing money fo
www.acmicpc.net

문제가 길지만 요약을 해보자면, 1일부터 365일까지 기간 중에 2개의 방에 대해 예약을 받을 때, 두 방을 합한 예약 비용이 최대가 되도록 했을 때 그 비용을 구하는 문제입니다.
우선 이전에 최소 비용 최대 유량 문제를 풀어봤더라도 어떤 노드를 어떻게 연결시켜야할지 고민이 될 수 있습니다.
이 문제에서는 번호에 대응되는 값이 날짜뿐이므로, 이를 활용하여 노드를 적절히 연결시키는 것이 중요합니다.
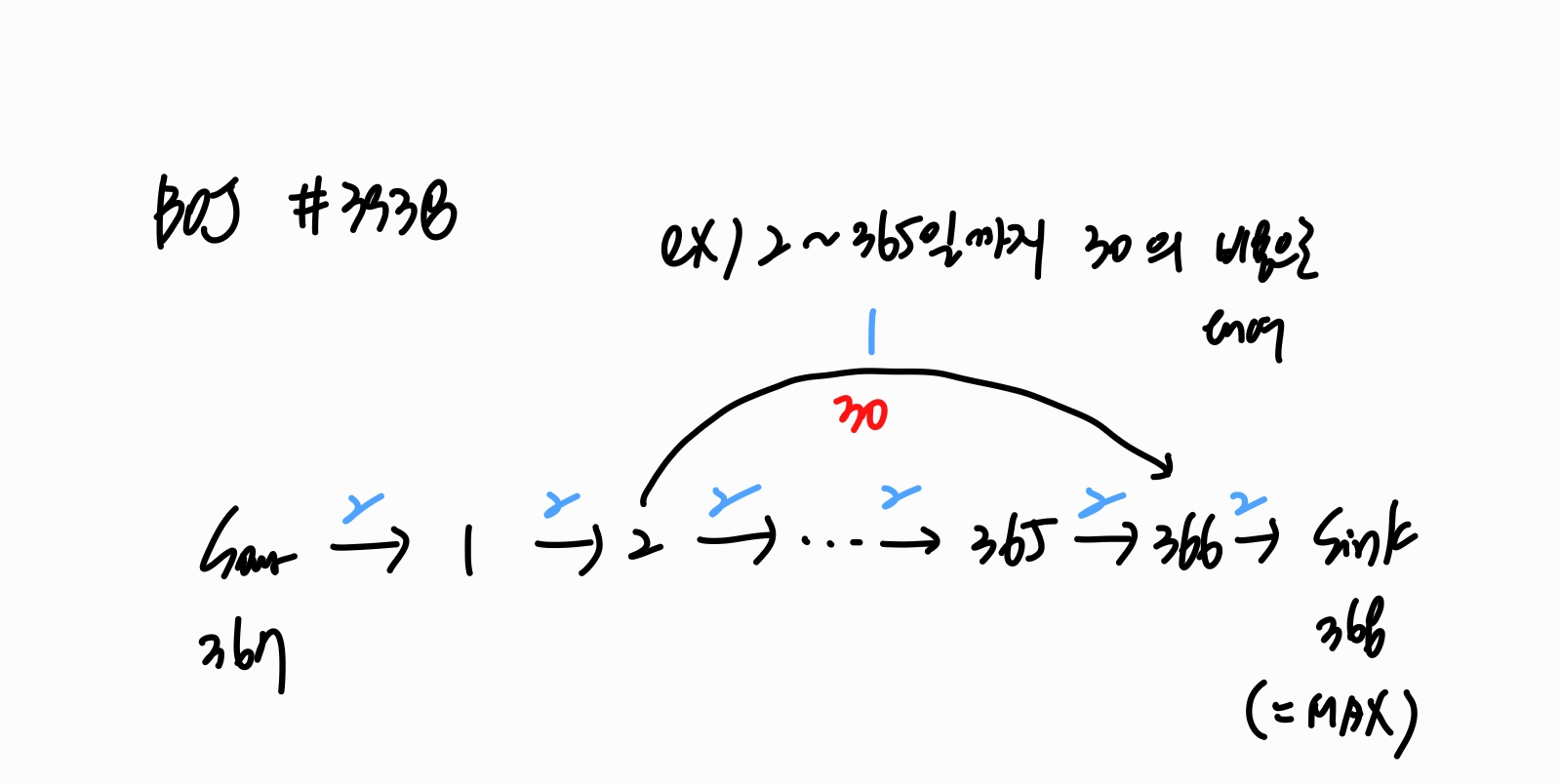
제가 문제를 해결하기 위해 구성한 그래프는 위와 같습니다.
노드 번호에 대응시킬만한 값이 날짜뿐이므로, 일 수를 노드로 연결하고 방은 2개가 존재하므로 유량을 2로 잡습니다.
그리고 예약에 대해서 시작일 ~ 종료일+1에 연결을 해주는데 이것은 방을 이용할 수 있게 되는 것은 종료일의 다음날부터이기 때문입니다.
따라서 위의 구현을 위해 종료일+1에 간선을 연결해주고 365일에 예약이 들어오는 경우도 있기 때문에 366번 노드까지 만들어서 일렬로 연결해주어야 합니다.

그리고 이 문제에는 예외가 있는데, 바로 같은 시작일과 종료일에 예약이 여러 개 존재하는 경우입니다.
이 경우 단순히 vector<int> Line[MAX]로 Line에 대한 벡터를 선언하여 풀이할 경우 해결책이 존재하지 않습니다.
왜냐하면 이렇게 구현한 경우 같은 시작점과 종료점을 가진 Line은 하나만 저장이 되기 때문입니다.
예를 들어 위와 같이 2일 ~ 4일에 걸쳐 예약이 1, 10, 100의 비용으로 3개가 들어왔다고 할 때, 답으로 110을 출력해야 하지만 잘못 구현할 경우 200이나 100이 나오게 됩니다.
따라서 이러한 문제의 경우 간선에 대한 연결 리스트를 구현하여 해결해주어야 합니다.
#include <cstdio>
#include <vector>
#include <queue>
#include <algorithm>
#define MAX 370
#define INF 1000000000
using namespace std;
struct Edge {
int From, To, Capacity, Cost, Flow;
Edge* Rev;
Edge(int U, int V, int Cap, int Co) : From(U), To(V), Capacity(Cap), Cost(Co), Flow(0) {}
int Remain() { return Capacity - Flow; }
void AddFlow(int Amount) {
Flow += Amount;
Rev->Flow -= Amount;
}
};
vector<Edge*> Line[MAX];
void AddLine(int From, int To, int Capacity, int Cost) {
Edge* E = new Edge(From, To, Capacity, Cost);
Edge* RevE = new Edge(To, From, 0, -Cost);
E->Rev = RevE, RevE->Rev = E;
Line[From].push_back(E), Line[To].push_back(RevE);
}
int MCMF(int Sour, int Sink) {
int CostSum = 0;
while(true) {
Edge* Prev[MAX]; fill(Prev, Prev+MAX, nullptr);
int Cost[MAX]; fill(Cost, Cost+MAX, INF); Cost[Sour] = 0;
queue<int> Queue; Queue.push(Sour);
bool isInQueue[MAX] = {}; isInQueue[Sour] = true;
while(!Queue.empty()) {
int Curr = Queue.front(); Queue.pop();
isInQueue[Curr] = false;
for(int i=0; i<Line[Curr].size(); i++) {
int Next = Line[Curr][i]->To;
if(Line[Curr][i]->Remain() > 0 && Cost[Curr] + Line[Curr][i]->Cost < Cost[Next]) {
Cost[Next] = Cost[Curr] + Line[Curr][i]->Cost;
Prev[Next] = Line[Curr][i]->Rev;
if(!isInQueue[Next]) {
Queue.push(Next);
isInQueue[Next] = true;
}
}
}
}
if(Prev[Sink] == nullptr) break;
int Amount = INF;
for(int i=Sink; i!=Sour; i=Prev[i]->To)
Amount = min(Prev[i]->Rev->Remain(), Amount);
for(int i=Sink; i!=Sour; i=Prev[i]->To) {
CostSum += -Prev[i]->Cost * Amount;
Prev[i]->AddFlow(-Amount);
}
}
return CostSum;
}
int main() {
int N, M, From, To, Cost;
while(1) {
scanf("%d", &N);
if(N == 0) break;
for(int i=0; i<MAX; i++) vector<Edge*>().swap(Line[i]);
int Sour = 367, Sink = 368;
AddLine(Sour, 1, 2, 0), AddLine(366, Sink, 2, 0);
for(int i=1; i<=365; i++) AddLine(i, i+1, 2, 0);
for(int i=0; i<N; i++) {
scanf("%d %d %d", &From, &To, &Cost);
AddLine(From, To+1, 1, -Cost);
}
printf("%d\n", -MCMF(Sour, Sink));
}
}
연결리스트를 이용한 구현 자체는 이전의 '학교 가지마!' 문제에서도 다루었으니 참고하시면 좋을 것 같습니다.
연결리스트의 구현 자체는 해당 문제와 동일합니다.
[백준/BOJ C++] 1420번 : 학교 가지마! (최대 유량 최소 컷 정리, 맵의 연결리스트 구현)
이 포스트는 프로그래밍 문제 사이트 백준 Online Judge(BOJ)의 1420번 : '학교 가지마!' 문제의 풀이 코드와 해설을 다루고 있습니다. 문제 난이도는 Solved.ac 기준 Platinum II에 해당하며, 문제를 풀이하
restudycafe.tistory.com
제출해보면 위와 같이 정답 처리를 받을 수 있습니다.
'알고리즘 > 백준(BOJ) 문제풀이' 카테고리의 다른 글
| [백준/BOJ C++] 11111번 : 두부장수 장홍준2 / 10937번 : 두부 모판 자르기 (MCMF) (0) | 2022.01.01 |
|---|---|
| [백준/BOJ C++] 10786번 : Catering (ACM-ICPC World Finals 2015 C번) (0) | 2021.12.31 |
| [백준/BOJ C++] 3640번 : 제독 (최소 비용 최대 유량 알고리즘) (0) | 2021.12.30 |
| [백준/BOJ C++] 2311번 : 왕복 여행 (최소 비용 최대 유량 알고리즘, MCMF) (0) | 2021.12.29 |
| [백준/BOJ C++] 1658번 : 돼지 잡기 (최대 유량, Network Flow) (1) | 2021.12.29 |