이 포스트는 프로그래밍 문제 사이트 백준 Online Judge의 1516번 : '게임 개발' 문제의 풀이 코드와 해설을 다루고 있습니다.
문제의 난이도는 Solved.ac 기준 Gold 티어에 해당하며, 문제를 풀이하기 위해 위상 정렬(Topological Sort)의 개념을 다룰 것입니다.
1516번 : 게임 개발
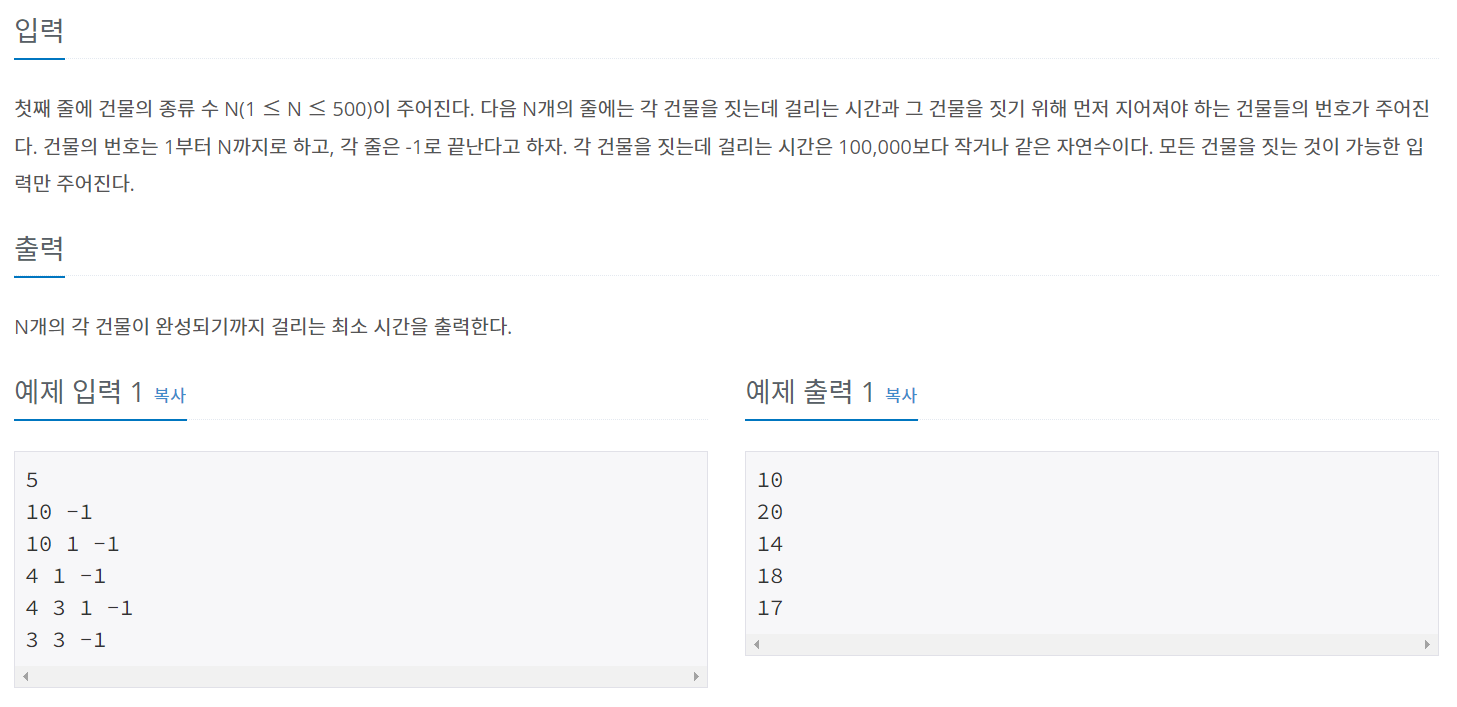
위와 같이 N개의 건물에 대해, 각 건물을 짓는 시간이 주어지고 그 건물을 짓기 위해 먼저 지어져야 하는 건물의 번호가 주어질 때, 각 건물이 완성되기까지 걸리는 최소 시간을 각각 출력하는 문제입니다.
건물의 번호들을 각 노드로 만들고, 선행 건물들을 연결하여 위상 정렬 알고리즘을 이용하여 해결할 수 있는 문제입니다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
|
#include <cstdio>
#include <vector>
#include <queue>
#define MAX 505
using namespace std;
int Degree[MAX], Time[MAX], Sum[MAX];
vector<int> Node[MAX];
queue<int> Queue;
int main() {
int N, X, Pop, Next;
scanf("%d", &N);
for(int i=1; i<=N; i++) {
scanf("%d", &Time[i]);
while(1) {
scanf("%d", &X);
if(X == -1) break;
Node[X].push_back(i);
Degree[i]++;
}
}
for(int i=1; i<=N; i++)
if(!Degree[i]) {
Queue.push(i);
Sum[i] = Time[i];
}
while(!Queue.empty()) {
Pop = Queue.front();
Queue.pop();
for(int i=0; i<Node[Pop].size(); i++) {
Next = Node[Pop][i];
if(Sum[Pop]+Time[Next] > Sum[Next]) Sum[Next] = Sum[Pop] + Time[Next];
Degree[Next]--;
if(!Degree[Next]) Queue.push(Next);
}
}
for(int i=1; i<=N; i++) printf("%d\n", Sum[i]);
}
|
cs |
선언된 변수들을 설명하자면, Degree는 선행 노드의 수를 저장하는 배열이고, Time은 각 건물이 지어지는데 걸리는 시간, Sum은 이 건물이 지어지는데까지 선행 노드까지 모두 합쳐서 걸리는 시간(출력 할 답)이 저장되는 배열입니다.
우선 각 건물이 지어지는 Time[i]를 저장하고, 그 다음 선행 건물의 번호 X를 입력받아 -1이면 아무 처리 없이 넘어가고 그게 아닐 경우 선행 노드로 연결을 해줍니다. Node[A].push_back[B]는 A에서부터 B로 연결되는 간선을 의미합니다.
입력이 완료된 이후에는 다시 1번 건물부터 확인하며 선행 노드가 없는 것들만 큐에 삽입합니다.
그리고 그 건물이 다른 건물의 선행 노드가 되는 간선들을 확인하면서 Sum을 갱신해주고, 간선이 제거된 이후 새롭게 발생하는 선행 노드가 없는 노드들을 큐에 다시 추가해줍니다.
마지막에는 이렇게 갱신된 Sum들을 모두 출력해주면 됩니다.

풀이를 제출해보면 간단히 정답을 인정받을 수 있습니다.
딱히 예외가 발생할만한 문제도 아니어서 위상 정렬의 개념만 알면 쉽게 해결할 수 있었습니다.
2056번 : 작업

N개의 작업에 대해, 각 작업 번호 순서대로 작업을 수행하는데 걸리는 시간과 그 작업보다 먼저 수행되어야 하는 선행 작업의 번호들이 주어질 때, 모든 작업을 완료하는데 걸리는 시간을 구하는 문제입니다.
이 역시 선행 작업들을 연결하여 풀이하는 문제이므로 위상 정렬로 해결할 수 있습니다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
|
#include <cstdio>
#include <vector>
#include <queue>
#define MAX 10005
using namespace std;
int Degree[MAX], Time[MAX], Sum[MAX];
vector<int> Node[MAX];
queue<int> Queue;
int main() {
int N, M, X, Pop, Next, Max = 0;
scanf("%d", &N);
for(int i=1; i<=N; i++) {
scanf("%d %d", &Time[i], &M);
for(int j=0; j<M; j++) {
scanf("%d", &X);
Node[X].push_back(i);
Degree[i]++;
}
}
for(int i=1; i<=N; i++)
if(!Degree[i]) {
Queue.push(i);
Sum[i] = Time[i];
}
while(!Queue.empty()) {
Pop = Queue.front();
Queue.pop();
for(int i=0; i<Node[Pop].size(); i++) {
Next = Node[Pop][i];
if(Sum[Pop]+Time[Next] > Sum[Next]) Sum[Next] = Sum[Pop] + Time[Next];
Degree[Next]--;
if(!Degree[Next]) Queue.push(Next);
}
}
for(int i=1; i<=N; i++)
if(Sum[i] > Max) Max = Sum[i];
printf("%d", Max);
}
|
cs |
코드 자체는 위의 문제와 아주 비슷한 것이, 선행 작업이라는 개념 자체가 위의 문제와 동일하기 때문입니다.
시간을 Time 배열에 저장해주고, 큐에 선행 노드가 없는 것들을 먼저 대입 시켜서 간선들을 제거해가며 Sum을 구해줍니다.
모든 간선이 제거된 이후 가장 큰 Sum을 출력하면 그것이 마지막 작업이 수행되는데까지 걸린 시간의 누적합이므로 총 소요 시간이 됩니다.

풀이 제출 결과는 위와 같이 얻어짐을 확인할 수 있습니다.
'알고리즘 > 백준(BOJ) 문제풀이' 카테고리의 다른 글
| [C++ 백준 풀이][Bronze IV] 외국어 문제들 번역 풀이 (0) | 2021.12.15 |
|---|---|
| [C++ 백준 풀이][Bronze IV] 20499, 19698, 18408, 19602, 21598, 18411, 18414, 20673, 20976, 18330번 풀이 (0) | 2021.12.15 |
| [백준] Solved.ac 플레티넘 티어 달성과 후기 (0) | 2021.12.15 |
| [C++ 백준 풀이] 2699번 : 격자점 컨벡스헐 / 6194번 : Building the Moat / 10903번 : Wall construction (0) | 2021.12.15 |
| [C++ 백준 풀이][Platinum] 1708번 : 볼록 껍질 (Convex Hull 알고리즘) (1) | 2021.12.14 |