이 포스트에서는 프로그래밍 문제 사이트 백준 Online Judge의 1182번 : '부분수열의 합 1'과 1208번 : '부분수열의 합 2'의 풀이 코드와 해설을 다루고 있습니다.
문제의 난이도는 Solved.ac 기준 1182번 : '부분수열의 합 1'은 Silver, 1208번 : '부분수열의 합 2'는 Gold 티어에 해당하며, 이 포스트에서는 Gold 티어 문제를 기준으로 풀이를 작성하겠습니다.
이 문제를 풀이하는데 필요한 알고리즘은 이분 탐색과 재귀적 탐색입니다.
부분수열의 합 문제는 N개의 정수로 이루어진 수열에서 일부 수열을 선택하여 해당 수열의 합이 S가 되는 경우의 수를 구하는 문제입니다.
부분수열의 합 1과 2 문제는 아예 같지만 N이 20 이하이거나 40 이하로 그 범위가 다릅니다.
부분수열의 합 1은 백트래킹만 가지고 해결이 가능하지만, 부분수열의 합 2는 백트래킹만으로는 시간 초과가 발생하며 따라서 이분 탐색을 이용해서 탐색을 수행해주어야 합니다.
여기서는 두 문제를 공통으로 해결할 수 있는, '부분수열의 합 2' 문제의 풀이를 중점적으로 정리하도록 하겠습니다.
1208번 : 부분수열의 합 2
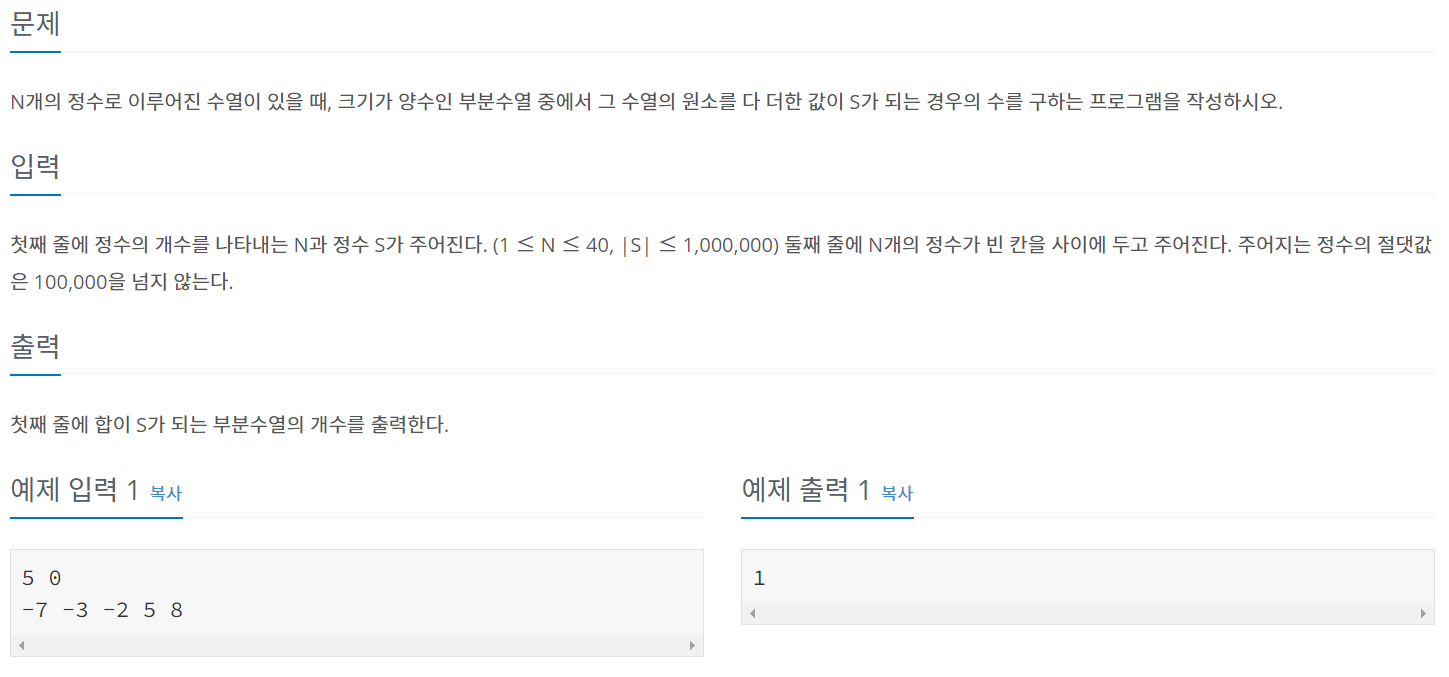
문제의 예제에서는 오름차순으로 입력이 들어오는 것으로 보이지만, 문제의 조건을 보면 오름차순으로 입력이 된다는 조건은 없으므로 정렬된 데이터를 사용하는 것이 아님을 알 수 있습니다.
N이 40이고, 각 원소에 대해 선택을 하냐 안하냐의 두 가지 선택지가 있기 때문에, 브루트포스 알고리즘으로 이 문제를 해결하면 O(2^40)의 시간이 걸리게 되어 시간 초과가 발생합니다.
따라서 이를 해결하기 위해 이분 탐색을 사용하도록 하겠습니다.

↓ 위의 이미지와 동일한 풀이 코드는 아래의 접은 글에 정리되어 있습니다.
#include <cstdio>
#include <vector>
#include <map>
using namespace std;
int N, S;
long long ans = 0;
vector<int> arr;
map<int, int> cnt;
void left_search(int left, int right, int sum) {
if(left == right) {
cnt[sum]++;
return;
}
left_search(left+1, right, sum);
left_search(left+1, right, sum+arr[left]);
}
void right_search(int left, int right, int sum) {
if(left == right) {
if(cnt[S-sum]) ans += cnt[S-sum];
else if(sum == S) ans++;
return;
}
right_search(left+1, right, sum);
right_search(left+1, right, sum+arr[left]);
}
int main() {
scanf("%d %d", &N, &S);
arr.resize(N);
for(int i=0; i<N; i++) scanf("%d", &arr[i]);
left_search(0, N/2, 0);
right_search(N/2, N, 0);
if(!S) ans--;
printf("%lld", ans);
}
풀이의 핵심 아이디어는 40개 이하의 원소를 2개의 그룹으로 나누어 각각 탐색을 수행하는 것입니다.
그렇게 되면 최대치인 40개의 데이터가 입력되어도 O(2^20 + 2^20)으로 훨씬 짧은 시간에 해결이 가능함을 알 수 있습니다.
우선 arr를 입력받고, left_search와 right_search를 나누어 탐색을 수행합니다.
각각의 search 함수는 left부터 선택을 해가면서 arr[left+1]을 선택을 하는 경우와 안하는 경우 두 가지를 나누어 재귀적으로 다시 탐색을 수행하게 합니다.
탐색이 끝났을 때 sum 값의 해시값을 1 증가시켜서, sum이 나오는 경우의 수를 count 해줍니다.
이후 right_search에 대해서도 같은 방식으로 탐색을 수행하되, 여기서는 left_search에서 구한 sum값과 합해서 S가 되는 것이 있는지를 확인해 줍니다.
만약 있으면 해당 해시값을 더해서 ans에 더해주면 됩니다.
또한 한 쪽 그룹 내에서만 더해서 S 값이 나오는 경우도 있기 때문에 그러한 경우도 cnt를 해줄 수 있도록 합니다.
위의 코드를 이용해 예제를 테스트해보면 1이 아니라 2가 나옴을 알 수 있는데, 그것은 S 값이 0일 때 아무 원소도 선택하지 않는 경우도 경우의 수에 포함시켰기 때문입니다.
따라서 S=0인 경우는 ans 값을 1 감소시켜서 출력해주어야 합니다.

코드를 제출해보면 920ms로 거의 아슬아슬하게 통과가 됨을 알 수 있습니다.
이러한 경우는 cin, cout을 그냥 사용하면 처리가 느려져서 통과를 못할수도 있기 때문에 입출력부도 빠른 처리를 할 수 있도록 코드를 작성해주는 것이 좋습니다.
1182번 : 부분수열의 합 1
부분수열의 합 1 문제는 위의 문제와 다르게 N이 20 이하로 주어집니다.
이 경우는 그냥 모든 경우를 다 탐색해도 제한 시간 안에 해결이 가능하기 때문에 그냥 풀어도 되지만, 위의 문제와 같은 코드를 제출해도 역시 통과가 됩니다.
'알고리즘 > 백준(BOJ) 문제풀이' 카테고리의 다른 글
| [C++ 백준 풀이] 2042번 : 구간 합 구하기 (세그먼트 트리, Segment Tree) (0) | 2021.12.10 |
|---|---|
| [C++ 백준 풀이][Gold IV] 2473번 : 세 용액 (투 포인터 알고리즘 응용) (0) | 2021.12.09 |
| [C++ 백준 풀이][Gold III] 1005번 : ACM Craft / 2623번 : 음악프로그램 (위상 정렬 응용) (0) | 2021.12.09 |
| [C++ 백준 풀이] 1197번 : 최소 스패닝 트리 / 1647번 : 도시 분할 계획 (크루스칼 알고리즘) (0) | 2021.12.09 |
| [C++ 백준 풀이][Gold] 2252번 : 줄 세우기 / 1766번 : 문제집 (위상 정렬) (0) | 2021.12.09 |