이 포스트에서는 프로그래밍 문제 사이트 백준 Online Judge의 '1644번 : 소수의 연속합', '17404번 : RGB거리 2' 문제에 대한 풀이 코드와 해설을 다루고 있습니다.
문제의 난이도는 Solved.ac 기준 '소수의 연속합'은 Gold III, 'RGB거리 2'는 Gold IV에 해당합니다.
두 문제에 필요한 배경 지식으로는 '소수의 연속합'은 두 포인터 알고리즘, 'RGB거리 2'는 동적 프로그래밍 개념이 필요하며 이 포스트에서 다룰 것입니다.
1644번 : 소수의 연속합

자연수 N에 대해 연속된 소수들을 나열하고 구간 합을 구할 때, 그 합이 N인 조합의 수를 출력하는 문제입니다.
소수의 오름차순 나열은 정해져 있는 값이기 때문에, 소수를 빠르게 구해주고 이들의 구간 합을 계산하는 알고리즘을 효율적으로 작성하는 문제입니다.
구간 합을 계산하는 문제이기 때문에 a번째 원소 ~ b번째 원소의 합을 sum[b] - sum[a-1]로 구하는 방식도 있겠으나, 여기서는 경우의 수를 구해야 하기 때문에 이 방법으로는 어렵고 두 포인터 알고리즘을 활용하는 것이 효율적입니다.
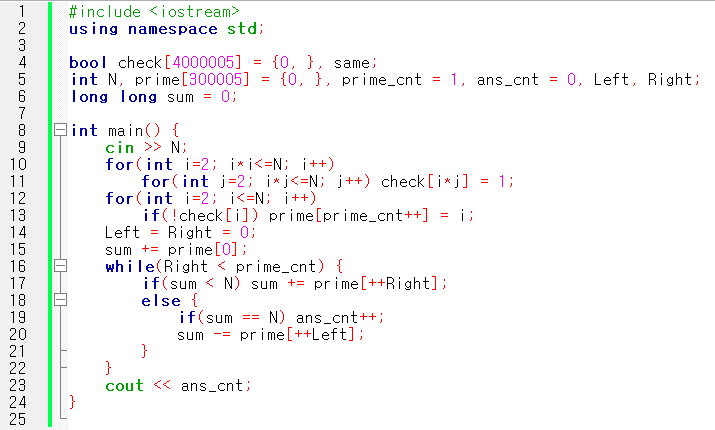
↓ 위의 이미지와 동일한 풀이 코드는 아래 접은 글에 정리되어 있으니 참고해 주세요.
#include <iostream>
using namespace std;
bool check[4000005] = {0, }, same;
int N, prime[300005] = {0, }, prime_cnt = 1, ans_cnt = 0, Left, Right;
long long sum = 0;
int main() {
cin >> N;
for(int i=2; i*i<=N; i++)
for(int j=2; i*j<=N; j++) check[i*j] = 1;
for(int i=2; i<=N; i++)
if(!check[i]) prime[prime_cnt++] = i;
Left = Right = 0;
sum += prime[0];
while(Right < prime_cnt) {
if(sum < N) sum += prime[++Right];
else {
if(sum == N) ans_cnt++;
sum -= prime[++Left];
}
}
cout << ans_cnt;
}
풀이를 보면 우선 N이 400만 이하이기 때문에 소수를 빠르게 구해주기 위해서 에라토스테네스의 체를 활용하였습니다.
i*i <= N인 i에 대해 N보다 작은 i*j를 모두 체크해주고 체크가 안된 소수들만 빠르게 정리하는 알고리즘입니다.
이후 left와 right를 둘 다 0으로 잡아주고, 다음의 경우에 따라 처리를 다르게 해줍니다.
( i ) sum이 N보다 작은 경우 : right을 1 증가시켜서 sum에 더해 sum을 증가시킵니다.
( ii ) sum이 N과 같은 경우 : ans_cnt를 1 증가시켜 경우의 수를 세어주고, left를 1 증가시켜서 sum에서 빼서 sum을 감소시킵니다.
( iii ) sum이 N보다 큰 경우 left를 1 증가시켜서 sum에서 빼서 sum을 감소시킵니다.
위의 세 가지 경우대로 수행을 하다보면 합이 N이 되는 모든 구간을 찾을 수 있으며 탐색이 종료되면 Right가 구간 끝에 도달하게 됩니다.
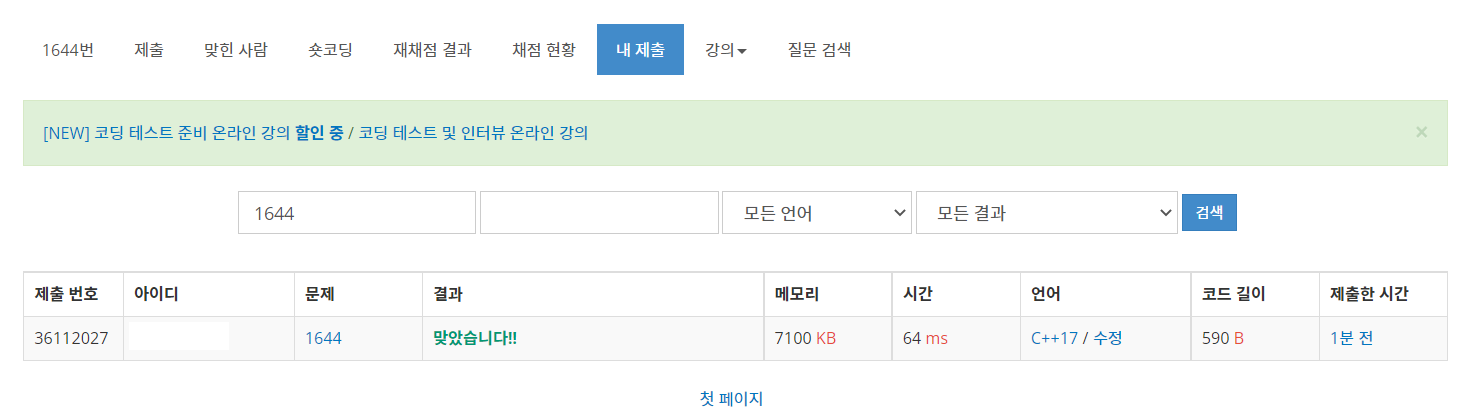
위의 코드를 제출해서 채점해보면 64ms의 시간에 모든 테스트케이스를 통과했음을 확인할 수 있습니다.
모든 경우의 수를 탐색했으면 O(N^2)의 시간이 소요됨을 생각해보면 두 포인터 알고리즘이 얼마나 효율적인지 알 수 있습니다.
17404번 : RGB거리 2
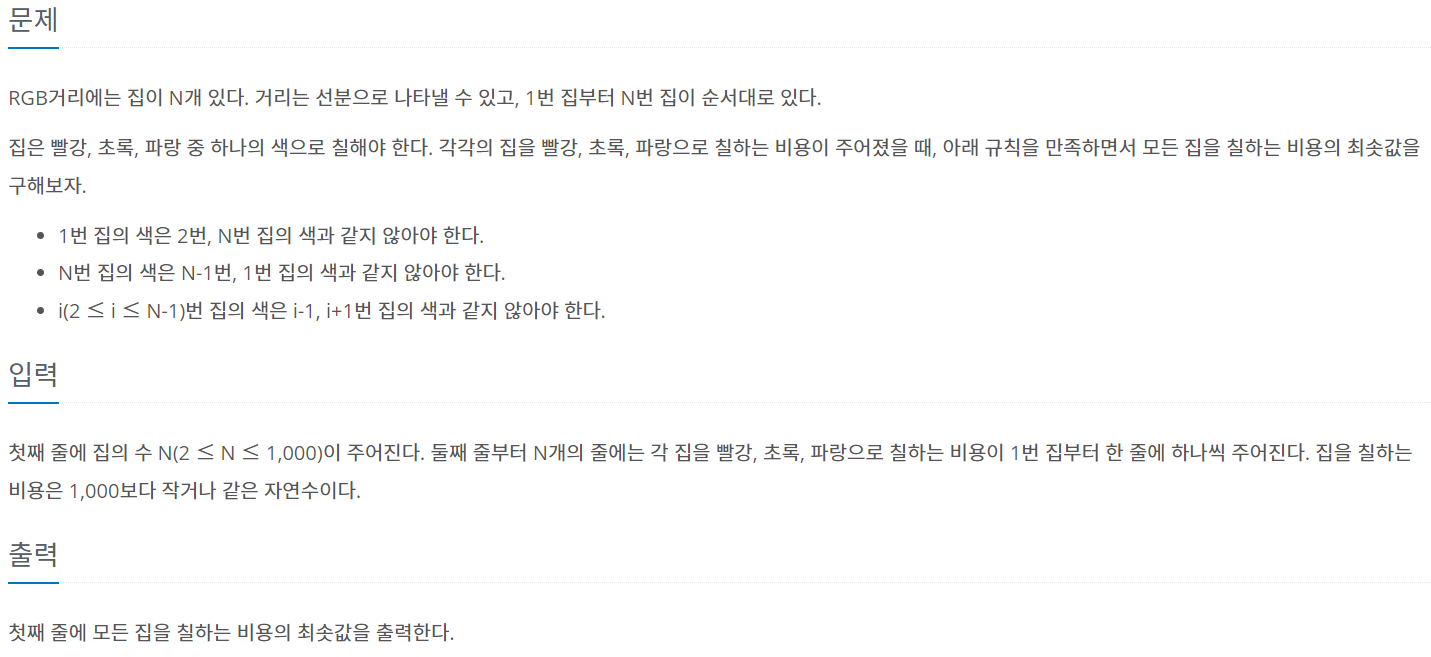
이 문제는 RGB거리 1 문제에서 더 심화된 문제입니다.
N개의 집이 양 왼쪽과 오른쪽 집과 색을 다르게 선택할 때, 주어진 비용들을 참고하여 모든 집들을 칠하는 비용의 최소 합을 구하는 문제입니다.
참고로 RGB거리 1 문제는 1번 집과 N번 집은 각각 왼쪽 집과 오른쪽 집의 색을 신경쓸 필요가 없었으나, 이 문제에서는 원순열과 같이 1번 집은 N번 집의 색을, N번 집은 1번 집의 색을 신경써야 합니다.
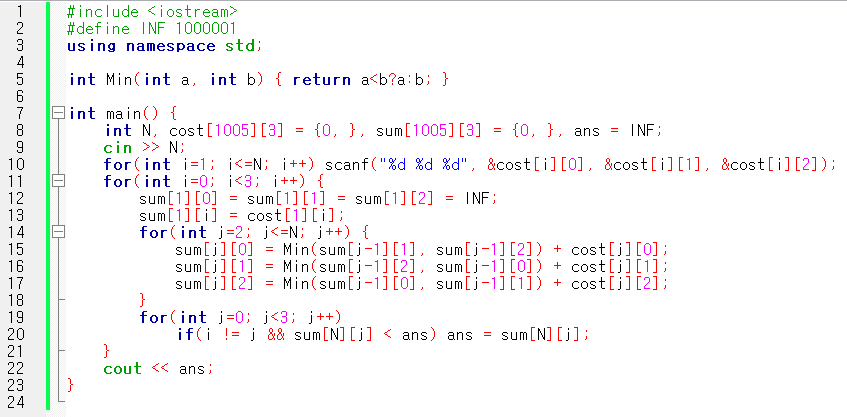
↓ 위의 이미지와 동일한 풀이 코드는 아래 접은 글에 정리되어 있습니다.
#include <iostream>
#define INF 1000001
using namespace std;
int Min(int a, int b) { return a<b?a:b; }
int main() {
int N, cost[1005][3] = {0, }, sum[1005][3] = {0, }, ans = INF;
cin >> N;
for(int i=1; i<=N; i++) scanf("%d %d %d", &cost[i][0], &cost[i][1], &cost[i][2]);
for(int i=0; i<3; i++) {
sum[1][0] = sum[1][1] = sum[1][2] = INF;
sum[1][i] = cost[1][i];
for(int j=2; j<=N; j++) {
sum[j][0] = Min(sum[j-1][1], sum[j-1][2]) + cost[j][0];
sum[j][1] = Min(sum[j-1][2], sum[j-1][0]) + cost[j][1];
sum[j][2] = Min(sum[j-1][0], sum[j-1][1]) + cost[j][2];
}
for(int j=0; j<3; j++)
if(i != j && sum[N][j] < ans) ans = sum[N][j];
}
cout << ans;
}
풀이는 기존 문제에 비해 생각보다 복잡해지는데, 그 이유는 N번 집을 선택할 때 1번 집이 어떤 색을 칠했는지 dp 배열에 저장을 안해주기 때문입니다.
따라서 1번 집에 어떤 색을 칠했는지에 따라 모든 경우의 수를 나누기 위해 바깥쪽 loop를 한 개 더 만들어줍니다.
예를 들어 i=0일 때는 1번 집을 red로 칠하는 경우가 됩니다.
1번 집을 red로 고정시키기 위해서는, green과 blue로 칠하는 cost 값을 INF로 설정하여 무조건 red가 선택되게 만들어줍니다. (sum[1] 값들을 모두 INF로 설정하고, i 값에 따라 해당 색만 원래대로 돌려서 최솟값이 되도록 설정)
그리고 마지막 집을 선택할 때 i와 다른 j의 색으로 칠함으로써 1번 집과 N번 집의 색을 다른 색으로 선택할 수 있습니다.
위의 풀이 코드를 제출해보면 거의 시간이 소요되지 않고 모든 테스트케이스를 통과함을 확인할 수 있습니다.
DP와 더불어 간단한 풀이 아이디어 또한 필요한 문제였습니다.
'알고리즘 > 백준(BOJ) 문제풀이' 카테고리의 다른 글
| [C++ 백준 풀이] 1197번 : 최소 스패닝 트리 / 1647번 : 도시 분할 계획 (크루스칼 알고리즘) (0) | 2021.12.09 |
|---|---|
| [C++ 백준 풀이][Gold] 2252번 : 줄 세우기 / 1766번 : 문제집 (위상 정렬) (0) | 2021.12.09 |
| [C++ 백준 풀이][Gold II] 1007번 : 벡터 매칭 (재귀함수 + 벡터 연산 기법) (0) | 2021.12.09 |
| [C++ 백준 풀이][Gold IV] 2239번, 2580번 : 스도쿠 (백트래킹) (0) | 2021.12.09 |
| [C++ 백준 풀이] 2166번 : 다각형의 면적 (사선 공식, CCW 알고리즘) (0) | 2021.12.08 |