이 포스트는 프로그래밍 문제 사이트 백준 Online Judge의 플로이드-워셜(Floyd-Warshall) 알고리즘을 사용하는 문제인 11403번 : 경로 찾기에 대한 풀이 코드와 해설을 포함하고 있습니다.
Class 3의 에센셜 문제들 중에서도 그래프 문제를 많이 안 풀고 있었는데 그 중에서도 플로이드 워셜 알고리즘을 사용해볼 수 있는 문제를 풀이해보도록 하겠습니다.
플로이드 워셜 알고리즘은 한 정점에서 다른 정점으로 이동이 가능한지를 확인할 때 사용되는 알고리즘으로, i에서 k로 갈 수 있고 k에서 j로 갈 수 있다면 i에서 j로 갈 수 있다는 원리를 이용한 알고리즘입니다.
11403번 : 경로 찾기

문제를 보면, 양방향이 아닌 단방향 그래프가 총 N개의 줄에 걸쳐서 연결 유무가 입력될 때, 노드 i에서 노드 j로 이동이 가능한지 여부를 나타내는 배열을 출력하는 문제입니다.
위의 예제에서 보면 노드 1에서 노드 2로 이동이 가능하고, 노드 2에서 노드 3으로 이동이 가능하며, 노드 3에서 노드 1로 이동이 가능하므로 결국 모든 노드 사이에 이동이 가능하다는 의미이므로 출력은 모든 칸이 1로 나오도록 만들어주어야 합니다.
예제 출력을 보면 원리대로 출력이 제대로 나왔음을 확인할 수 있습니다.
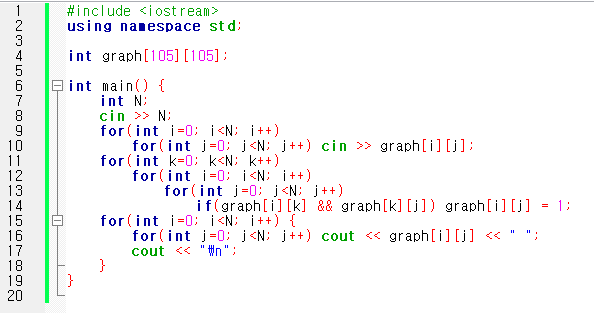
↓ 복사가 가능한 풀이 코드는 아래의 접은 글에 정리되어 있습니다.
#include <iostream>
using namespace std;
int graph[105][105];
int main() {
int N;
cin >> N;
for(int i=0; i<N; i++)
for(int j=0; j<N; j++) cin >> graph[i][j];
for(int k=0; k<N; k++)
for(int i=0; i<N; i++)
for(int j=0; j<N; j++)
if(graph[i][k] && graph[k][j]) graph[i][j] = 1;
for(int i=0; i<N; i++) {
for(int j=0; j<N; j++) cout << graph[i][j] << " ";
cout << "\n";
}
}
이제 풀이 코드를 확인해보면, 우선은 N을 입력받고 나서 그래프의 연결 상태를 입력받아야 합니다.
이를 graph 배열에 저장하도록 했으며, 이제 각 연결 관계를 이용하여 이동이 가능한지를 살펴보아야 합니다.
플로이드-워셜 알고리즘을 사용하여 k를 돌려서 i에서 j 사이에 k가 연결되어 있는지 아닌지를 3중 for문을 이용하여 확인해줍니다.
이 때 k가 돌아가는 루프를 가장 안쪽에 넣을 경우 3중 for문을 돌려도 한 다리 건너서 갈 수 있는지까지밖에 확인이 안되기 때문에 반드시 k를 가장 바깥쪽 루프에 배치시켜야 합니다.
k 루프를 가장 바깥쪽에 배치시키면 i, j 루프가 먼저 돌아가면서 노드 1을 통해서 i에서 j로 갈 수 있는지, 노드 2를 통해서 갈 수 있는지, 노드 3을 통해서 갈 수 있는지를 순서대로 체크해 가면서 모든 경우를 확인할 수 있게 됩니다.

풀이 코드를 제출해보면 위와 같이 정답임을 확인할 수 있으며, 3중 for문임에도 크기가 100 이하인 그래프가 주어졌기 때문에 채점 소요 시간이 4ms 밖에 되지 않음을 알 수 있습니다.
Floyd-Warshall 알고리즘은 O(N^3)이라는 오래 걸리는 알고리즘이기 때문에 N이 커졌을 때는 시간을 보장하지 못해 다른 알고리즘을 사용해야 한다는 단점이 있습니다.
'알고리즘 > 백준(BOJ) 문제풀이' 카테고리의 다른 글
| [C++ 백준 풀이] cin, cout과 scanf, printf 차이점 (11659번 : 구간 합 구하기 4) (0) | 2021.12.03 |
|---|---|
| [C++ 백준 풀이][Gold IV] 2206번 : 벽 부수고 이동하기 (조건이 추가된 BFS) (0) | 2021.12.03 |
| [C++ 백준 풀이] 10866번 : 덱 (Deque, 덱 직접 구현해보기) (0) | 2021.12.02 |
| [C++ 백준 풀이] 1927번 : 최소 힙 / 11279번 : 최대 힙 (Priority Queue 활용) (0) | 2021.12.02 |
| [C++ 백준 풀이] 15829번 : Hashing / 11866번 : 요세푸스 문제 0 / 1676번 : 팩토리얼 0의 개수 (0) | 2021.12.02 |