이 포스트는 프로그래밍 문제 사이트 백준 Online Judge의 '1167번 : 트리의 지름'과 '1967번 : 트리의 지름' 두 문제에 대한 풀이 코드와 해설을 다루고 있습니다.
트리의 지름을 구하는 원리에 대해 설명하기 위해 작성하였고, 두 문제는 비슷한 번호와 동일한 이름만을 가지고 있을 뿐 다른 문제임을 알려드립니다.
두 가지의 비슷한 문제들을 풀어보면서, 트리의 지름을 어떻게 구하는지 설명드리겠습니다.
1167번 : 트리의 지름

먼저 1167번 문제입니다.
문제에서 정의하는 트리의 지름이란, 간선의 길이 또는 비용이 가장 먼 두 점을 잇는 길이나 비용을 의미합니다.
즉, 트리의 루트 노드에서 가장 먼 두 지점이 양 트리 지름의 끝 점이 될 것입니다.
이 문제에서는 입력이 주어질 때, 각 노드의 번호 순서대로 연결된 노드와 간선의 길이가 입력되며, 이 수는 제한이 없습니다.
다만 입력이 끝나면 -1으로 행 입력의 종료를 알려줍니다.
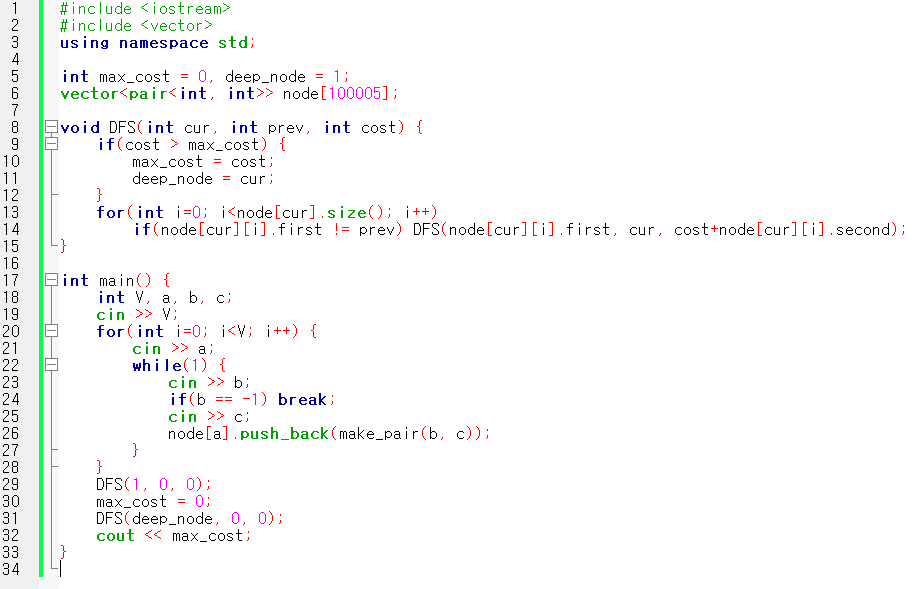
#include <iostream>
#include <vector>
using namespace std;
int max_cost = 0, deep_node = 1;
vector<pair<int, int>> node[100005];
void DFS(int cur, int prev, int cost) {
if(cost > max_cost) {
max_cost = cost;
deep_node = cur;
}
for(int i=0; i<node[cur].size(); i++)
if(node[cur][i].first != prev) DFS(node[cur][i].first, cur, cost+node[cur][i].second);
}
int main() {
int V, a, b, c;
cin >> V;
for(int i=0; i<V; i++) {
cin >> a;
while(1) {
cin >> b;
if(b == -1) break;
cin >> c;
node[a].push_back(make_pair(b, c));
}
}
DFS(1, 0, 0);
max_cost = 0;
DFS(deep_node, 0, 0);
cout << max_cost;
}
핵심 아이디어는, 루트 노드에서 가장 먼 두 노드를 찾는 것입니다.
그렇게 하기 위해서는, 루트에서 가장 깊은 노드를 한 번 찾은 뒤, 그 노드에서 탐색해서 가장 먼 노드를 다시 한 번 찾아주어야 합니다.
우리는 루트 노드는 입력을 통해 바로 연결해서 찾을 수 있기 때문에, 첫 탐색을 루트에서 시작하는 것이 가장 좋습니다.
앞선 포스트에서도 설명한 적이 있지만 트리 그래프는 연결 간선의 수가 그렇게 많지 않기 때문에 배열에 트리의 연결 관계를 저장하는 것은 메모리 측면에서 굉장히 비효율적입니다.
또한 메모리를 많이 사용하기 때문에 이 문제에 한해서는 메모리 초과가 발생하기도 합니다.
따라서 vector를 이용하여 각 node에 간선이 입력될 때마다 push_back해서 맨 뒤에 원소들을 추가해줍니다.
연결 관계에 대한 정보 입력이 끝났으면 루트 노드인 1번 노드에서 DFS를 시작해서, 최대 cost가 소모되는 노드를 찾습니다.
찾은 이후에는 max_cost를 0으로 초기화 시키고 해당 노드에서 다시 DFS를 시작하여 최대 cost가 소모되는 노드를 찾아줍니다.
이 두 노드 사이의 거리가 트리의 지름이므로, 두 번째로 DFS를 했을 때의 max_cost를 출력해주면 됩니다.

풀이 시간을 보면 생각보다 짧은 시간에 풀리는 것은 아니라는 사실을 알 수 있습니다.
그렇기에 더욱 시간적 효율이 중요한 문제였습니다.
1967번 : 트리의 지름

다음은 문제의 이름은 동일하지만 조금 다른 '트리의 지름' 문제를 풀어보겠습니다.
이 문제는 노드의 수를 알려주지 않고 대신 간선의 수를 미리 알려줍니다.
간선의 수만큼 노드의 쌍과 비용을 입력받고, 트리의 지름을 찾는 문제입니다.
#include <iostream>
#include <vector>
using namespace std;
int max_cost = 0, deep_node = 1;
vector<pair<int, int>> node[100005];
void DFS(int cur, int prev, int cost) {
if(cost > max_cost) {
max_cost = cost;
deep_node = cur;
}
for(int i=0; i<node[cur].size(); i++)
if(node[cur][i].first != prev) DFS(node[cur][i].first, cur, cost+node[cur][i].second);
}
int main() {
int N, a, b, c;
cin >> N;
for(int i=0; i<N-1; i++) {
cin >> a >> b >> c;
node[a].push_back(make_pair(b, c));
node[b].push_back(make_pair(a, c));
}
DFS(1, 0, 0);
max_cost = 0;
DFS(deep_node, 0, 0);
cout << max_cost;
}
문제가 다르지만, 사실 위의 1167번 문제를 해결한 코드에서 거의 바꾸지 않고도 해결이 가능합니다.
우선 입력부를 수정해주고, 그 다음 가장 중요한 부분은 입력을 하나 받을 때마다 양 노드에 모두 서로의 연결 정보를 입력해주어야 한다는 것입니다.
트리의 지름을 찾는 문제에서는 하위 노드로만 이동하는 것이 아니라, 상위 노드로도 이동을 해야하기 때문입니다.

코드를 제출해서 채점해보면 훨씬 빠른 시간에 정답 처리가 된 것을 확인할 수 있습니다.
아무래도 위의 문제에 비해 테스트케이스의 크기가 작은 것으로 보입니다.
'알고리즘 > 백준(BOJ) 문제풀이' 카테고리의 다른 글
| [C++ 백준 풀이] 15829번 : Hashing / 11866번 : 요세푸스 문제 0 / 1676번 : 팩토리얼 0의 개수 (0) | 2021.12.02 |
|---|---|
| [C++ 백준 풀이] 1436번 : 영화감독 숌 / 1966번 : 프린터 큐 / 2164번 : 카드2 (우선 순위 큐, priority queue) (0) | 2021.12.02 |
| [C언어 백준 풀이][Gold V] 15686번 : 치킨 배달 (재귀함수, 브루트포스 알고리즘) (0) | 2021.12.01 |
| [C언어 백준 풀이] 5639번 : 이진 검색 트리 (연결리스트 구조체로 트리 구현) (0) | 2021.12.01 |
| [C++ 백준 풀이] 11725번 : 트리의 부모 찾기 (벡터 활용) (0) | 2021.12.01 |