드디어 백준 solved.ac의 Bronze에서 가장 어려운 난이도인 Bronze I까지 도달했습니다.
Bronze 난이도의 문제는 저번에 다루었던 유클리드 호제법 응용 문제 빼고는 딱히 어려운 문제가 없어 빨리 다음 단계로 넘어가기를 희망합니다.
여기서는 1032번 : 명령 프롬프트, 1110번 : 더하기 사이클, 1145번 : 적어도 대부분의 배수 이렇게 3문제를 다루도록 하겠습니다.
1032번 : 명령 프롬프트
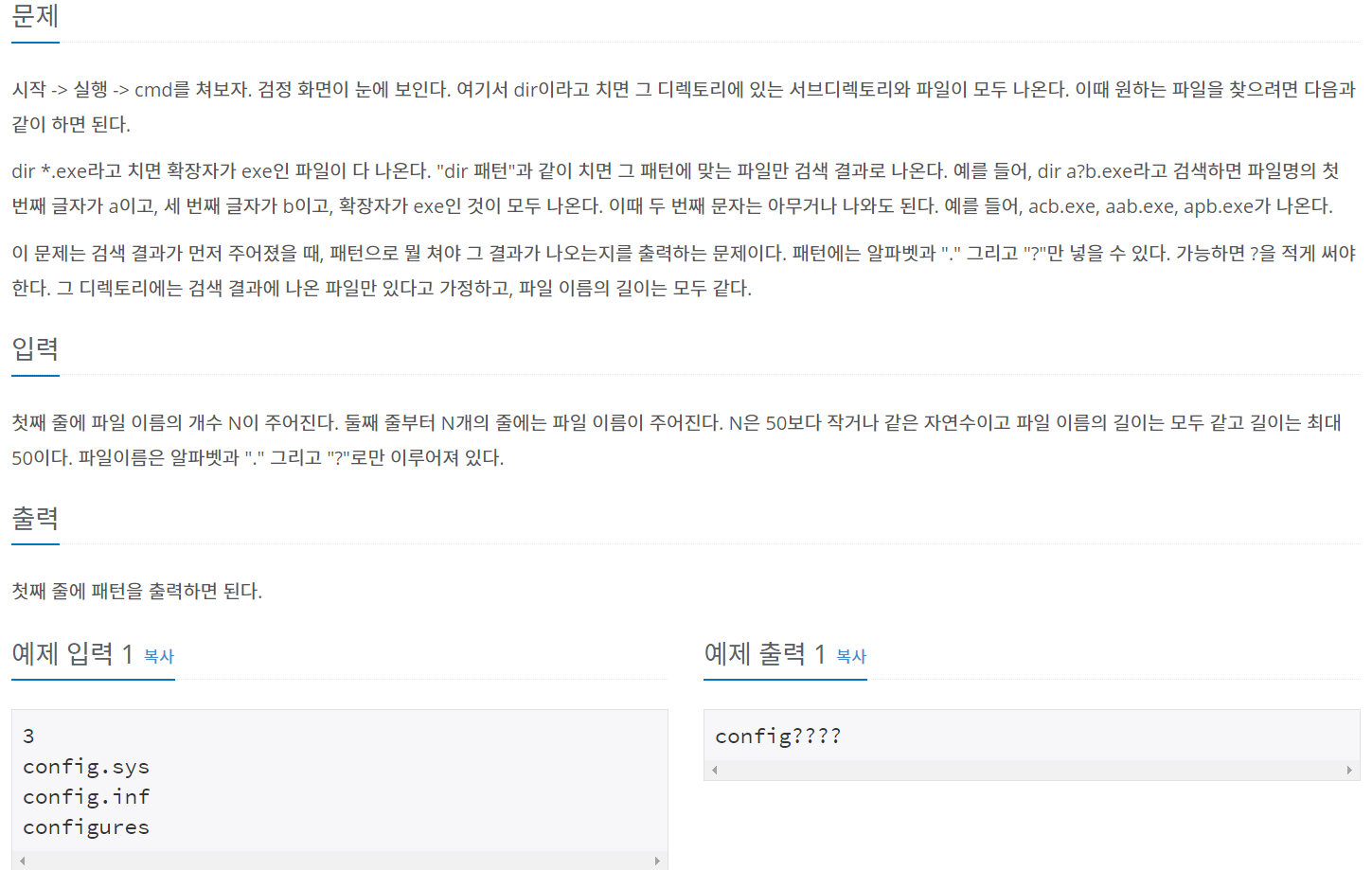
명령 프롬프트의 파일 조건문 검색 명령어를 기반으로 만들어진 문제입니다.
실제로 명령 프롬프트 조건문 명령은 생각보다 다양하지만, 이 문제는 그 기능과는 아예 별개로 만들어진 문제라고 생각하면 됩니다.
문자열의 길이를 따질 필요도 없고, 그냥 몇 번째 문자끼리가 서로 일치하는지 그 여부만 찾으면 되는 문제입니다.
또한 문자열의 최대 개수는 50개, 최대 길이도 50자이므로 시간의 제약없이 자유롭게 작성할 수 있습니다.
#include<stdio.h>
int main() {
int n, check;
char name[51][51], output[51];
scanf("%d", &n);
for(int i=0; i<n; i++) scanf("%s", name[i]);
for(int j=0; j<51; j++) {
check = 1;
for(int i=1; i<n; i++) if(name[i][j] != name[0][j]) check = 0;
if(check) output[j] = name[0][j];
else output[j] = '?';
}
printf("%s", output);
}
제 풀이는 위와 같습니다.
간단하게 name에 대한 2차원 char 배열을 선언해주고, input을 우선 받습니다.
이후 검사를 할 때 모든 문자열의 n번째 자리가 같다 = 첫 번째 문자열의 n번째 자리와 나머지 문자열의 n번째 자리가 같다는 성질을 이용하여 그냥 첫 번째 문자열을 기준으로 잡고 나머지 문자열들의 해당 자리가 같은지 검사합니다.
만약 하나라도 다르다면, 체크포인트를 변경하여 기록해줍니다.
마지막에 조건문을 만들어 체크포인트가 여전히 1이라면 모든 문자열의 n번째 자리가 같은 것이므로 출력문에도 같은 문자를 출력해주고, 아니라면 '?' 문자로 변경하여 출력해줍니다.
1110번 : 더하기 사이클
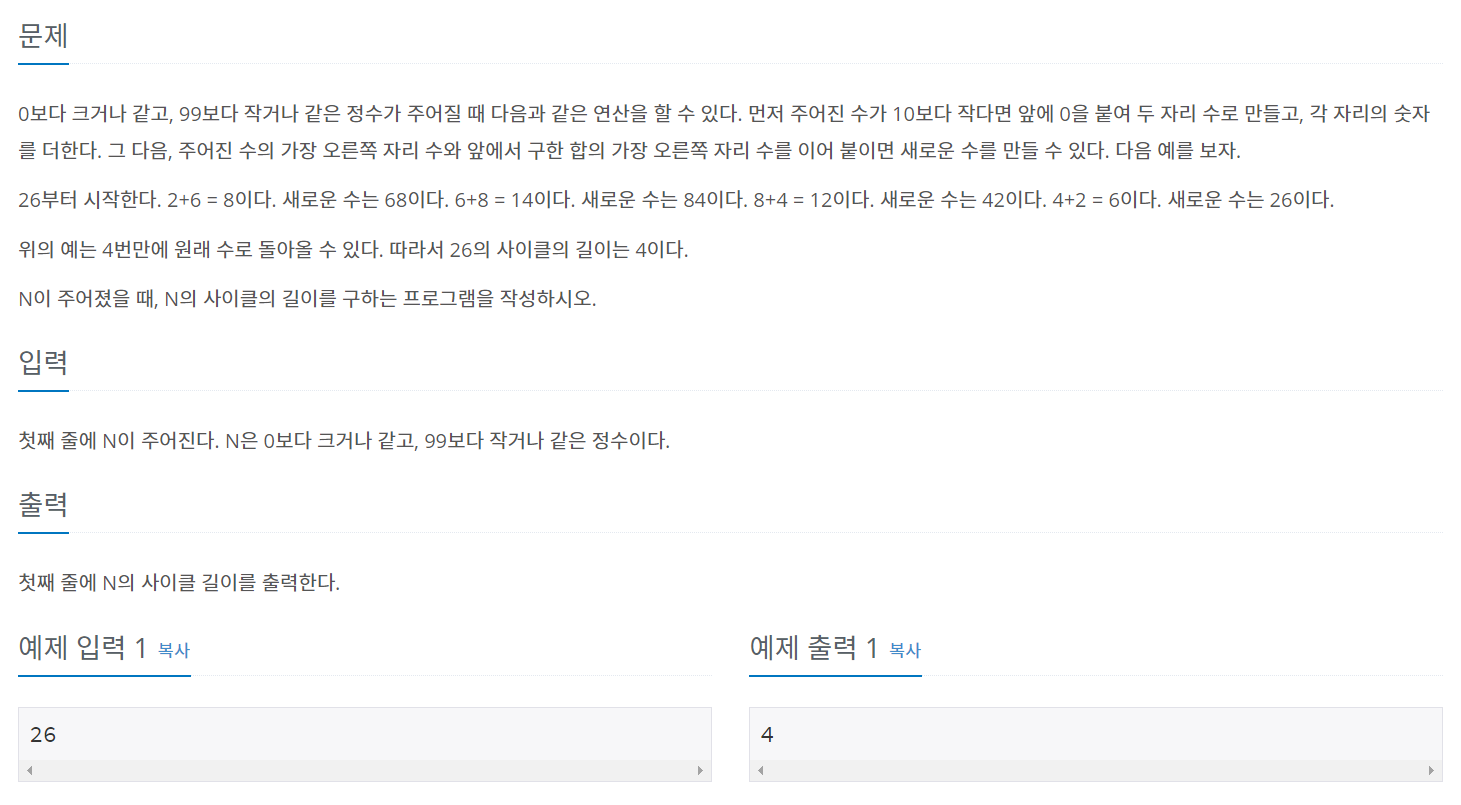
더하기 사이클이라는 이 문제에서 제시하는 규칙대로 연산 + 반복문만 돌려주면 풀 수 있는 문제입니다.
자연수를 십의 자리와 일의 자리로 쪼개서 일의 자리는 십의 자리로 옮기고, 십의 자리와 일의 자리를 더한 수의 일의 자리를 일의 자리로 옮겨서 새로운 숫자를 만들 때, 원래 수로 돌아오기 위한 연산의 횟수를 구하면 됩니다.
#include<stdio.h>
int main() {
int n, m, i=0;
scanf("%d", &n);
m = n;
while(1) {
m = m%10*10 + (m/10 + m%10)%10;
i++;
if(m == n) break;
}
printf("%d", i);
}
m = m%10*10 + (m/10 + m%10)%10; 부분을 식 하나로 쓰기에는 복잡해보일 수 있으나, 십의 자리에 어떤 수가 와야하고 일의 자리에 어떤 수가 와야하는지 천천히 생각하면 어렵지 않게 풀 수 있는 문제입니다.
또한 n을 입력받은 뒤 m으로 따로 옮겨야 초기에 입력받은 n과 비교하여 break 문을 구현할 수 있습니다.
1145번 : 적어도 대부분의 배수

이 문제에서 정의하는 '적어도 대부분의 배수'란 최소공배수와는 다른 개념으로, 5개의 자연수 중 3개 이상의 자연수에 대해 최소공배수가 되는 수를 의미합니다.
따라서 이 문제에서 내린 정의에 따라 최소공배수를 다른 방식으로 구해야 합니다.
#include<stdio.h>
int main() {
int n[6], ans = 1, check;
for(int i=0; i<5; i++) scanf("%d", &n[i]);
while(1) {
check = 0;
for(int i=0; i<5; i++) if(ans%n[i] == 0) check++;
if(check >= 3) break;
ans++;
}
printf("%d", ans);
}
5C3 = 10밖에 안되기 때문에 그냥 10가지 조건문을 모두 작성할까 했는데, 아무래도 일반화된 문제를 풀기 좋은 방법으로 접근하는 편이 코딩 역량을 기르는 면에서는 더 유용할 것 같아 check 변수를 이용했습니다.
ans를 1부터 시작하여 늘려가면서 5개의 자연수 중 한 개로 나누어떨어질 때마다 check를 1씩 증가시키고, 매 루프마다 검사하여 이것이 3 이상일 경우 루프를 탈출하도록 하였습니다.
또한 이 때 while문에서 무한 루프가 걸리는지 검사도 해주어야 하는데, 최소공배수는 아무리 커도 세 수의 곱보다는 커질 수 없기 때문에 무한 루프에 걸릴 일이 없습니다.